2021-2022学年北京三十五中高一（上）月考数学试卷（12月份）

一.选择题（共12个小题，每题3分，共36分。每小题只有一个正确选项，请选择正确答案填在机读卡相应的题号处）

• 1．已知全集U=R，集合P={x|x²≤1}，那么∁_UP=（　　）

  A．（-∞，-1]	B．[1，+∞）
  C．[-1，1]	D．（-∞，-1）∪（1，+∞）
  组卷：552引用：23难度：0.9

  解析

• 2．在同一坐标系中，函数y=2^x与y=

  （

  1

  2

  ）

  x

  的图象之间的关系是（　　）

  A．关于y轴对称	B．关于x轴对称
  C．关于原点对称	D．关于直线y=x对称
  组卷：396引用：28难度：0.9

  解析

• 3．给定函数①

  y

  =

  x

  1

  2

  ，②y=

  log

  1

  2

  （x+1），③y=x²-4x+1，④y=2^x+1，其中在区间（0，1）上单调递减的函数序号是（　　）

  A．①②

  B．③④

  C．②③

  D．①④
  组卷：34引用：1难度：0.8

  解析

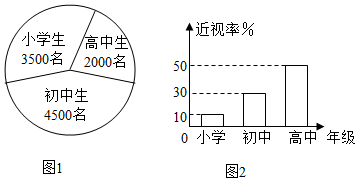• 4．已知某地区中小学生人数和近视情况分别如图1和图2所示．为了了解该地区中小学生的近视形成原因，用分层抽样的方法抽取2%的学生进行调查，则样本容量和抽取的高中生近视人数分别为（　　）

  A．200，20

  B．100，20

  C．200，10

  D．100，10
  组卷：1471引用：47难度：0.9

  解析

• 5．下列各对向量中，共线的是（　　）

  A． a =（2，3）， b =（3，-2）	B． a =（2，3）， b =（4，-6）
  C． a =（ 2 ，-1）， b =（1， 2 ）	D． a =（1， 2 ）， b =（ 2 ，2）
  组卷：514引用：6难度：0.9

  解析

• 6．函数f（x）=（m²-m-1）

  x

  m

  2

  -

  m

  -

  3

  是幂函数，且在区间（0，+∞）上是减函数，则实数m为（　　）

  A．1

  B．-1

  C．2

  D．-1或2
  组卷：7引用：1难度：0.7

  解析

• 7．下列大小关系正确的是（　　）

  A．0.42＜30.4＜log40.3	B．0.42＜log40.3＜30.4
  C．log40.3＜0.42＜30.4	D．log40.3＜30.4＜0.42
  组卷：10引用：1难度：0.8

  解析

三、解答题（本大题共5小题，共60分，解答时写出必要的文字说明、证明过程或演算步骤）

• 22．已知函数f（x）=log₃

  1

  +

  x

  1

  -

  x

  ．
  （1）求函数的定义域．
  （2）判断f（x）的奇偶性．
  （3）判断f（x）的单调性（只写出结论即可），并求当-

  1

  2

  ≤

  x

  ≤

  4

  5

  时，函数f（x）的值域．
  组卷：102引用：5难度：0.7

  解析

• 23．定义域为R的单调函数f（x）满足f（x+y）=f（x）+f（y）（x,y∈R），且f（3）=6，
  （1）求f（0），f（1）；
  （2）判断函数f（x）的奇偶性，并证明；
  （3）若对于任意

  x

  ∈

  [

  1

  2

  ，

  3

  ]

  都有f（kx²）+f（2x-1）＞0成立，求实数k的取值范围．
  组卷：59引用：1难度：0.4

  解析