2022-2023学年湖北省襄阳市樊城区八年级（下）期末数学试卷

一、选择题（本大题共10小题，每小题3分，共30分）

• 1．下列各代数式中，是二次根式的是（　　）

  A．-5

  B． 2

  C． a

  D． 3 6
  组卷：110引用：3难度：0.8

  解析

• 2．下列计算正确的是（　　）

  A． 3 + 2 = 5	B． 8 - 2 = 2
  C． （ - 4 ） × （ - 9 ） = - 4 × - 9 =6	D． （ - 4 ） 2 =-4
  组卷：50引用：1难度：0.7

  解析

• 3．“赵爽弦图”巧妙地利用面积关系证明了勾股定理，是我国古代数学的骄傲，如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成一个大正方形，设直角三角形较长直角边长为a,较短直角边长为b,若ab=24，大正方形的面积为129，则小正方形的边长为（　　）

  A．9

  B．10

  C．11

  D．12
  组卷：595引用：7难度：0.5

  解析

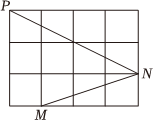• 4．如图，每个小正方形的边长为1，点P、M、N是小正方形的顶点，则∠PNM度数是（　　）

  A．30°

  B．40°

  C．45°

  D．60°
  组卷：91引用：2难度：0.5

  解析

• 5．下列命题中，是真命题的有（　　）
  ①对角线互相平分的四边形是平行四边形
  ②对角线互相垂直的四边形是菱形
  ③四边相等的平行四边形是正方形
  ④四角相等的四边形是矩形

  A．①②

  B．①④

  C．②③

  D．③④
  组卷：30引用：1难度：0.7

  解析

• 6．如图，菱形ABCD面积为24，对角线AC=8，DE⊥AB于点E，则DE=（　　）

  A．3

  B．4

  C． 12 5

  D． 24 5
  组卷：121引用：2难度：0.5

  解析

• 7．已知y=（2m-1）x

  m

  2

  -

  3

  是正比例函数，且y随x的增大而减小，那么这个函数的解析式为（　　）

  A．y=-5x

  B．y=5x

  C．y=3x

  D．y=-3x
  组卷：2337引用：11难度：0.9

  解析

• 8．正比例函数y=kx（k≠0）的函数值y随着x增大而减小，则一次函数y=x+k的图象大致是（　　）

  A．

  B．

  C．

  D．
  组卷：2979引用：50难度：0.8

  解析

三、解答题（本大题共9小题，共72分）

• 24．如图，在矩形ABCD中，AB=6，BC=8，动点E从点A出发，沿边AD，DC向点C运动，A，D关于直线BE的对称点分别为M，N，连结MN．
  （1）如图，当E在边AD上且DE=2时，求∠AEM的度数．
  （2）当N在BC延长线上时，求DE的长，并判断直线MN与直线BD的位置关系，说明理由．
  （3）当直线MN恰好经过点C时，求DE的长．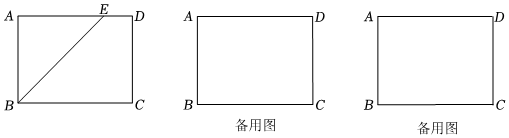
  组卷：2756引用：5难度：0.4

  解析

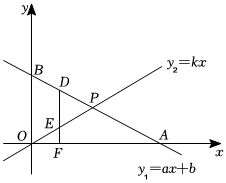• 25．如图，在平面直角坐标系中，一次函数y₁=ax+b的图象与x轴，y轴交于A，B；与直线y₂=kx交于P（2，1），且PO=PA．
  （1）求点A的坐标；
  （2）求函数y₁，y₂的解析式；
  （3）点D为直线y₁=ax+b上一动点，其横坐标为t（t＜2），DF⊥x轴于点F，交y₂=kx于点E，且DF=2EF，求点D的坐标；
  （4）在（3）的条件下，如果点D在第一象限内，过点P的直线y=mx+n将四边形OBDE分为两部分，两部分的面积分别设为S₁，S₂．若

  1

  2

  ≤

  S

  1

  S

  2

  ≤2，直接写出m的取值范围．
  组卷：220引用：1难度：0.3

  解析