2022-2023学年江苏省徐州市睢宁高级中学附属学校九年级(下)月考数学试卷(3月份)
发布:2024/7/10 8:0:8
一、选择题(24分)
-
1.已知关于x的一元二次方程m(x-h)2-k=0(m,h,k均为常数且m≠0)的解是x1=2,x2=5,则关于x的一元二次方程m(x-h+1)2=k的解是( )
组卷:650引用:5难度:0.5 -
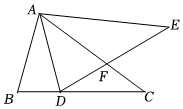 2.如图,在△ABC中,AB<AC,将△ABC以点A为中心逆时针旋转得到△ADE,点D在BC边上,DE交AC于点F.下列结论:①△AFE∽△DFC;②DA平分∠BDE;③∠CDF=∠BAD,其中所有正确结论的序号是( )组卷:2842引用:19难度:0.6
2.如图,在△ABC中,AB<AC,将△ABC以点A为中心逆时针旋转得到△ADE,点D在BC边上,DE交AC于点F.下列结论:①△AFE∽△DFC;②DA平分∠BDE;③∠CDF=∠BAD,其中所有正确结论的序号是( )组卷:2842引用:19难度:0.6 -
 3.如图,四边形ABCD内接于⊙O,AB是直径,OD∥BC,若∠C=124°,则∠B的度数为( )组卷:775引用:7难度:0.7
3.如图,四边形ABCD内接于⊙O,AB是直径,OD∥BC,若∠C=124°,则∠B的度数为( )组卷:775引用:7难度:0.7 -
4.如图1,在菱形ABCD中,∠A=60°,动点P从点A出发,沿折线AD→DC→CB方向匀速运动,运动到点B停止.设点P的运动路程为x,△APB的面积为y,y与x的函数图象如图2所示,则AB的长为( )
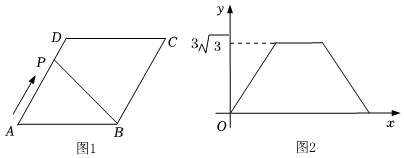 组卷:2437引用:29难度:0.6
组卷:2437引用:29难度:0.6 -
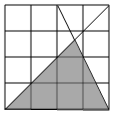 5.如图,若方格纸中每个小正方形的边长均为1,则阴影部分的面积为( )组卷:5578引用:40难度:0.7
5.如图,若方格纸中每个小正方形的边长均为1,则阴影部分的面积为( )组卷:5578引用:40难度:0.7 -
6.已知抛物线y=x2+kx-k2的对称轴在y轴右侧,现将该抛物线先向右平移3个单位长度,再向上平移1个单位长度后,得到的抛物线正好经过坐标原点,则k的值是( )
组卷:5110引用:28难度:0.5 -
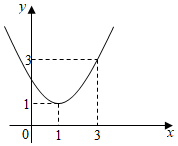 7.已知二次函数y=ax2+bx+c的图象如图所示,有下列结论:①a>0;②b2-4ac>0;③4a+b=0;④不等式ax2+(b-1)x+c<0的解集为1≤x<3,正确的结论个数是( )组卷:710引用:11难度:0.6
7.已知二次函数y=ax2+bx+c的图象如图所示,有下列结论:①a>0;②b2-4ac>0;③4a+b=0;④不等式ax2+(b-1)x+c<0的解集为1≤x<3,正确的结论个数是( )组卷:710引用:11难度:0.6 -
 8.如图,点P是函数y=(k1>0,x>0)的图象上一点,过点P分别作x轴和y轴的垂线,垂足分别为点A、B,交函数y=k1x(k2>0,x>0)的图象于点C、D,连接OC、OD、CD、AB,其中k1>k2.下列结论:①CD∥AB;②S△OCD=k2x;③S△DCP=k1-k22,其中正确的是( )(k1-k2)22k1组卷:3763引用:7难度:0.5
8.如图,点P是函数y=(k1>0,x>0)的图象上一点,过点P分别作x轴和y轴的垂线,垂足分别为点A、B,交函数y=k1x(k2>0,x>0)的图象于点C、D,连接OC、OD、CD、AB,其中k1>k2.下列结论:①CD∥AB;②S△OCD=k2x;③S△DCP=k1-k22,其中正确的是( )(k1-k2)22k1组卷:3763引用:7难度:0.5
二、填空(30)
-
9.高速公路便捷了物流和出行,构建了我们更好的生活.交通运输部的数据显示,截止去年底,我国高速公路通车里程161000公里,稳居世界第一.161000这个数据用科学记数法可表示为 .
组卷:304引用:5难度:0.8
三、解答题(86分)
-
27.已知,如图,二次函数y=ax2+bx-6的图象分别与x轴与y轴相交于点A(-6,0)、点B,点C(6,6)也在函数图象上.

(1)求该二次函数的解析式.
(2)动点P从点B出发,沿着y轴的正方向运动,是否存在某一位置使得∠OAP+∠OAC=45°?若存在,请求出点P的坐标;若不存在,请说明理由.
(3)点Q为直线AC下方抛物线上一点,当以点A、B、C、Q为顶点的四边形的面积最大时,求出点Q的坐标.组卷:1028引用:2难度:0.3 -
28.已知,点E、F、G、H分别在正方形ABCD的边AB、BC、CD、AD上.
(1)如图1,当四边形EFGH是正方形时,求证:AE+AH=AB;
(2)如图2,已知AE=AH,CF=CG,当AE、CF的大小有 关系时,四边形EFGH是矩形;
(3)如图3,AE=DG,EG、FH相交于点O,OE:OF=4:5,已知正方形ABCD的边长为16,FH长为20,当△OEH的面积取最大值时,判断四边形EFGH是怎样的四边形?证明你的结论.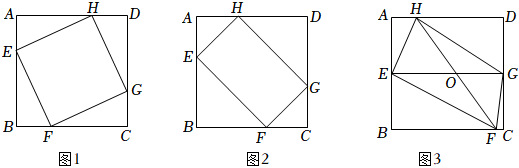 组卷:2082引用:4难度:0.1
组卷:2082引用:4难度:0.1


