2022-2023学年黑龙江省鹤岗一中高二（上）期中数学试卷

一、单选题（本题共8小题，每小题5分，共40分）

• 1．已知直线l经过点P（2，1），且与直线2x+3y+1=0垂直，则直线l的方程是（　　）

  A．2x+3y+1=0

  B．3x+2y-8=0

  C．2x-3y-1=0

  D．3x-2y-4=0
  组卷：8引用：1难度：0.8

  解析

• 2．如果方程x²+ky²=1表示焦点在x轴上的椭圆，那么实数k的取值范围（　　）

  A．（-∞，1）	B．（1，+∞）
  C．（0，1）	D．（-∞，0）∪（1，+∞）
  组卷：125引用：5难度：0.8

  解析

• 3．已知双曲线

  x

  2

  a

  2

  -

  y

  2

  b

  2

  =

  1

  （

  a

  ＞

  0

  ，

  b

  ＞

  0

  ）

  的一条渐近线方程是

  3

  x+y=0，它的一个焦点在抛物线y²=24x的准线上，则双曲线的方程为（　　）

  A． x 2 9 - y 2 27 = 1	B． x 2 27 - y 2 9 = 1
  C． x 2 36 - y 2 108 = 1	D． x 2 108 - y 2 36 = 1
  组卷：153引用：4难度：0.9

  解析

• 4．台风中心从M地以每小时30km的速度向西北方向移动，离台风中心30

  3

  km内的地区为危险地区，城市N在M地正西方向60km处，则城市N处于危险区内的时长为（　　）

  A．1h

  B． 2 h

  C．2h

  D．3h
  组卷：64引用：7难度：0.6

  解析

• 5．过点M（-1，

  1

  2

  ）的直线l与椭圆x²+2y²=2交于A，B两点，设线段AB的中点为M，设直线l的斜率为k₁（k₁≠0），直线OM的斜率为k₂，则k₁k₂的值为（　　）

  A．2

  B．-2

  C． 1 2

  D．- 1 2
  组卷：49引用：2难度：0.9

  解析

• 6．已知双曲线C：

  x

  2

  a

  2

  -

  y

  2

  b

  2

  =1（a＞0，b＞0）的左、右焦点分别为F₁，F₂，O为坐标原点，点M在C的右支上运动，△MF₁F₂的内心为I，若|IO|=|IF₂|，则C的离心率为（　　）

  A．2

  B． 2

  C．3

  D． 3
  组卷：49引用：4难度：0.4

  解析

• 7．已知圆C：（x+1）²+（y-4）²=m（m＞0）和两点A（-2，0），B（1，0），若圆C上存在点P，使得|PA|=2|PB|，m的取值范围是（　　）

  A．[8，64]

  B．[9，64]

  C．[8，49]

  D．[9，49]
  组卷：225引用：10难度：0.7

  解析

四、解答题（本题共6道小题，共计70分.解答应写出文字说明，证明过程或演算步骤）

• 21．在平面直角坐标系xOy中，椭圆C：

  x

  2

  a

  2

  +

  y

  2

  b

  2

  =1（a＞b＞0）的左，右顶点分别为A，B．F是椭圆的右焦点，

  AF

  =3

  FB

  ，

  AF

  •

  FB

  =3．
  （1）求椭圆C的方程；
  （2）不过点A的直线l交椭圆C于M，N两点，记直线l,AM，AN的斜率分别为k,k₁，k₂．若k（k₁+k₂）=1，证明直线l过定点，并求出定点的坐标．
  组卷：390引用：16难度：0.5

  解析

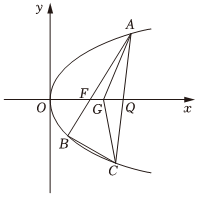• 22．如图，已知点F（1，0）为抛物线y²=2px（p＞0）的焦点．过点F的直线交抛物线于A，B两点，点A在第一象限，点C在抛物线上，使得△ABC的重心G在x轴上，直线AC交x轴于点Q，且Q在点F的右侧，记△AFG，△CQG的面积分别为S₁，S₂．
  （1）求p的值及抛物线的准线方程；
  （2）设A点纵坐标为2t,求

  S

  1

  S

  2

  关于t的函数关系式；
  （3）求

  S

  1

  S

  2

  的最小值及此时点G的坐标．
  组卷：52引用：2难度：0.5

  解析