当前位置：试卷中心 > 试卷详情

2023-2024学年北京166中九年级（上）期中数学试卷

发布：2024/9/29 17:0:13

一、选择题（本题共16分，每小题2分）第1-8题均有四个选项，符合

1．如图，AD∥BE∥CF，
AB
BC
=
1
2
，则
DE
EF
的值为（　　）
A．2 B．
1
2
C．
1
3
D．3
组卷：93引用：1难度：0.7
解析
2．抛物线y=-5（x+2）²-6的顶点坐标是（　　）
A．（2，6） B．（-2，6） C．（2，-6） D．（-2，-6）
组卷：796引用：13难度：0.9
解析
3．已知∠A是锐角，
tan
A
=
3
，那么∠A的度数是（　　）
A．15° B．30° C．45° D．60°
组卷：332引用：5难度：0.8
解析
4．将抛物线y=-2x²+1向右平移1个单位长度，再向上平移1个单位长度所得的抛物线解析式为（　　）
A．y=-2（x+1）² B．y=-2（x+1）²+2
C．y=-2（x-1）²+2 D．y=-2（x-1）²+1
组卷：1467引用：65难度：0.9
解析
5．将一元二次方程x²-8x+10=0通过配方转化为（x+a）²=b的形式，下列结果中正确的是（　　）
A．（x-4）²=6 B．（x-8）²=6 C．（x-4）²=-6 D．（x-8）²=54
组卷：1829引用：37难度：0.6
解析
6．如图，△ABC在网格（小正方形的边长均为1）中，则cos∠ABC的值是（　　）
A．
3
4
B．
4
3
C．
3
5
D．
4
5
组卷：743引用：8难度：0.7
解析
7．设A（-2，y₁），B（1，y₂），C（3，y₃）是抛物线y=x²+2x-9上的三点，则y₁，y₂，y₃的大小关系为（　　）
A．y₁＞y₂＞y₃ B．y₁＞y₃＞y₂ C．y₃＞y₂＞y₁ D．y₂＞y₁＞y₃
组卷：114引用：2难度：0.5
解析
8．用绳子围成周长为10m的矩形，记矩形的一边长为x m,它的邻边长为y m,矩形的面积为S m²，当x在一定范围内变化时，y和S都随x的变化而变化，则y与x、S与x满足的函数关系分别是（　　）
A．一次函数关系，二次函数关系
B．正比例函数关系，二次函数关系
C．二次函数关系，一次函数关系
D．正比例函数关系，一次函数关系
组卷：115引用：3难度：0.5
解析

二、填空题（本题共16分，每小题2分）

9．如图，在△ABC中，M，N分别为AB，AC的中点，若△AMN的面积是1，则△ABC的面积是
．
组卷：178引用：2难度：0.7
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

三、解答题（本题共68分，第17～-19、21题每小题5分，第20题6分，第22题5分，第23-24题，每小题5分，第25题5分，第26题6分，第27-28题，每小题5分）解答应写出文字说明、演算步骤或证明过程.

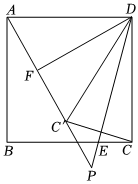27．如图，在正方形ABCD中，E是边BC上一动点（不与点B，C重合），连接DE，点C关于直线DE的对称点为C′，连接AC'并延长交直线DE于点P，F是AC′中点，连接DF．
（1）求∠FDP的度数；
（2）连接BP，请用等式表示AP，BP，DP三条线段之间的数量关系，并证明；
（3）若正方形的边长为
2
，请直接写出△ACC'的面积最大值．
组卷：367引用：6难度：0.3
解析
28．在平面直角坐标系xOy中，对于点P，直线l和矩形w,定义如下：若点P关于直线l的对称点P'在矩形ABCD的边上，则称点P为矩形ABCD关于直线l的“对矩点”．
已知矩形ABCD的顶点A（1，0），B（8，0），C（8，4），D（1，4）．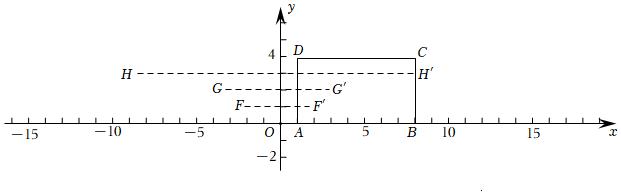

例如，图1中的点F和点G都不是矩形ABCD关于y轴的“对矩点”，点H是矩形ABCD关于y轴的“对矩点”．
（1）在点P₁（-2，2），P₂（2，4），P₃（4，2），P₄（6，3）中，是矩形ABCD关于直线l：x=3“对矩点”的点是
；
（2）若在直线y=2x+6上存在点M，使得点M是矩形ABCD关于直线l：x=t的“对矩点”，求t的取值范围；
（3）若抛物线y=-x²-4x+9上存在矩形ABCD关于直线l：x=t的“对矩点”且恰有4个，请直接写出t的取值范围．
组卷：520引用：5难度：0.2
解析