当前位置：试卷中心 > 试卷详情

2022-2023学年广东省佛山一中高二（下）期中数学试卷

发布：2024/5/24 8:0:9

一、单选题（本大题共8小题，共40.0分。在每小题列出的选项中，选出符合题目的一项）

1．用数学归纳法证明1+2+2²+…+2ⁿ⁺²＜2ⁿ⁺³（n∈N₊）时，第一步需要验证的不等式是（　　）
A．1＜2⁴ B．1+2＜2⁴
C．1+2+2²＜2⁴ D．1+2+2²+2³＜2⁴
组卷：119引用：2难度：0.8
解析
2．书架上有20本内容互不相同的书，其中6本数学书，4本语文书，10本英语书，从书架上任取两本书，则取出的两本书不同学科的方案数为（　　）
A．144种 B．124种 C．100种 D．84种
组卷：118引用：5难度：0.8
解析
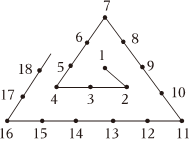3．将自然数1，2，3，4，5，……，按照如图排列，我们将2，4，7，11，16，……都称为“拐角数”，则下列哪个数不是“拐角数”．（　　）
A．22 B．30 C．37 D．46
组卷：20引用：4难度：0.8
解析
4．在当前市场经济条件下，私营个体商店中的商品，所标价格a与其实际价值之间，存在着相当大的差距．对顾客而言，总是希望通过“讨价还价”来减少商品所标价格a与其实际价值的差距．设顾客第n次的还价为b_n，商家第n次的讨价为c_n．有一种“对半讨价还价”法如下：顾客第一次的还价为标价a的一半，即第一次还价b₁=
a
2
，商家第一次的讨价为b₁与标价a的平均值，即c₁=
a
+
b
1
2
；⋯顾客第n次的还价为上一次商家的讨价c_n-1与顾客的还价b_n-1的平均值，即b_n=
c
n
-
1
+
b
n
-
1
2
，商家第n次的讨价为上一次商家的讨价c_n-1与顾客这一次的还价b_n的平均值，即c_n=
c
n
-
1
+
b
n
2
．现有一件衣服标价1200元，若经过n次的“对半讨价还价”，b_n与c_n相差不到2元，则n最小值为（　　）
A．4 B．5 C．6 D．7
组卷：23引用：1难度：0.6
解析
5．已知函数f（x）=x³-3x²存在对称中心，则f（x）在对称中心处的切线方程是（　　）
A．x+y+3=0 B．y-2=0 C．3x-y-6=0 D．3x+y-1=0
组卷：44引用：1难度：0.6
解析
6．已知函数f（x）=lnx,则下列错误的是（　　）
A．当x₂＞x₁＞1时，x₁f（x₁）＜x₂f（x₂）
B．当x₂＞x₁＞e时，x₂f（x₁）＞x₁f（x₂）
C．方程
f
（
x
）
x
=-1有两个不同的解
D．当x₂＞x₁＞0时，
f
（
x
1
）
-
f
（
x
2
）
x
1
-
x
2
＞
0
组卷：29引用：1难度：0.6
解析
7．“回文”是一种修辞手法，如“我为人人，人人为我”等，数学上具有这样特征的一类数称为“回文数”，“回文数”是指从左到右与从右到左读都一样的正整数，如121，241142等，在所有五位正整数中，有且仅有两位上的数字是奇数的“回文数”共有（　　）
A．100个 B．125个 C．225个 D．250个
组卷：74引用：1难度：0.5
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

四、解答题（本大题共6小题，共48.0分。解答应写出文字说明，证明过程或演算步骤）

21．已知等差数列{a_n}的前n项和记为S_n（n∈N^*），满足3a₂+2a₃=S₅+6．
（Ⅰ）若数列{S_n}为单调递减数列，求a₁的取值范围；
（Ⅱ）若a₁=1，在数列{a_n}的第n项与第n+1项之间插入首项为1，公比为2的等比数列的前n项，形成新数列{b_n}，记数列{b_n}的前n项和为T_n，求T₉₅．
组卷：317引用：5难度：0.5
解析
22．已知函数f（x）=e^x-1-mx²（m∈R）．
（1）当m=1，判断f（x）在区间（0，+∞）是否存在极小值点，并说明理由；
（2）已知m＞0，设函数g（x）=f（x）+mxln（mx）．若g（x）在区间（0，+∞）上存在零点，求实数m的取值范围．
组卷：28引用：2难度：0.5
解析