2023-2024学年重庆八中九年级（上）开学数学试卷

一.选择题（共10小题，满分40分，每小题4分）

• 1．下列各数中最大的是 （　　）

  A． - 1 2

  B．0

  C． 1 2

  D．2
  组卷：175引用：4难度：0.8

  解析

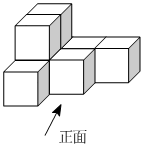• 2．如图是一个由8个相同的正方体组成的立体图形，它的主视图是（　　）

  A．

  B．

  C．

  D．
  组卷：556引用：10难度：0.8

  解析

• 3．反比例函数y=

  k

  x

  经过点（-1，-4），则反比例函数的解析式为（　　）

  A．y=-4x

  B．y= 4 x

  C．y=- 4 x

  D．y=4x
  组卷：651引用：5难度：0.7

  解析

• 4．若两个相似三角形的相似比为1：9，则这两个三角形的周长之比为（　　）

  A．1：3

  B．1：9

  C．1：27

  D．1：81
  组卷：372引用：3难度：0.7

  解析

• 5．如图，直线a∥b,∠1=55°，∠2=90°，则∠3的度数为（　　）
  ​

  A．35°

  B．40°

  C．45°

  D．55°
  组卷：152引用：5难度：0.7

  解析

• 6．甲、乙两种物质的溶解度y（g）与温度t（℃）之间的对应关系如图所示，则下列说法中，错误的是（　　）

  A．甲、乙两种物质的溶解度均随着温度的升高而增大

  B．当温度升高至t2℃时，甲的溶解度比乙的溶解度大

  C．当温度为0℃时，甲、乙的溶解度都小于20g

  D．当温度为30℃时，甲、乙的溶解度相等
  组卷：1358引用：23难度：0.8

  解析

• 7．估计

  （

  3

  18

  -

  12

  ）

  ÷

  3

  的值应该在（　　）

  A．3和4之间

  B．4和5之间

  C．5和6之间

  D．6和7之间
  组卷：1268引用：8难度：0.7

  解析

• 8．如图，用相同的小正方形按照某种规律进行摆放，则第8个图形中小正方形的个数是（　　）
  

  A．71

  B．78

  C．85

  D．89
  组卷：1792引用：24难度：0.7

  解析

三.解答题（共8小题，满分78分）

• 25．如图，已知点A（4，0）、B（0，2），线段OA=OC且点C在y轴负半轴上，连接AC．
  
  （1）求直线AB的解析式；
  （2）点P是直线CA上一点，连接BP，若S_△ABC=2S_△ABP，求满足条件的点P坐标；
  （3）点M为直线l：x=-

  5

  2

  上一点，将点M水平向右平移6个单位至点N，连接BM、MN．在平面内确定一点Q，使得以B、M、N、Q为顶点的四边形是菱形，写出符合所有条件的点Q的坐标，并写出求解点Q的坐标的其中一种情况的过程．
  组卷：357引用：1难度：0.1

  解析

• 26．在等腰直角△ABC中，∠ABC=90°，点D是边BC上一点，点E是边AC上一点，且满足CE=

  2

  BD，过点E作AD垂线，垂足为F，EF交CB延长线于点G．
  （1）如图1，若AB=4，BD=1，求线段BG的长．
  （2）如图2，将AC绕点A逆时针旋转得到AH，连接DH，若∠CAH+2∠ADB=180°，求证：AH+CE=

  2

  DH．
  （3）如图3，若AB=3，连接DE，以DE为斜边向左上方构造等腰直角△DEP，连接CP交DE于点Q，当DE取最小值时，请直接写出DQ的值．
  
  组卷：291引用：1难度：0.1

  解析