当前位置：试卷中心 > 试卷详情

2022-2023学年四川省广元市利州区东城实验学校九年级（上）第二次定时作业数学试卷

发布：2024/8/5 8:0:8

一、选择题（每小题3分，共30分）

1．下面的图形是用数学家名字命名的，其中既是轴对称图形又是中心对称图形的是（　　）
A．
斐波那契螺旋线 B．
笛卡尔心形线
C．
赵爽弦图 D．
科克曲线
组卷：1164引用：74难度：0.8
解析
2．下列运算正确的是（　　）
A．（a²）³=a⁸ B．a²•a³=a⁵
C．（-3a）²=6a² D．2a²b+3ab²=5a²b
组卷：15引用：4难度：0.6
解析
3．抛物线y=（x-1）（x+3）顶点坐标是（　　）
A．（2，5） B．（-22，-3） C．（1，0） D．（-1，-4）
组卷：67引用：3难度：0.9
解析
4．下列说法中，正确的是（　　）
A．长度相等的弧是等弧
B．圆的每一条直径都是它的对称轴
C．直径如果平分弦就一定垂直弦
D．直径所对的弧是半圆
组卷：1496引用：8难度：0.5
解析
5．关于二次函数y=（x-2）²+6的图象，下列结论不正确的是（　　）
A．抛物线的开口向上
B．x＜2时，y随x的增大而减小
C．对称轴是直线x=2
D．抛物线与y轴交于点（0，6）
组卷：1006引用：11难度：0.5
解析
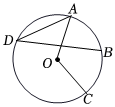6．如图，点A，B，C，D在⊙O上，∠AOC=140°，B是弧AC的中点，则∠D的度数是（　　）
A．30° B．35° C．45° D．70°
组卷：287引用：4难度：0.7
解析
7．如图，△ABC中，点D、E分别在AB、AC上，且
AD
DB
=
AE
EC
=
1
2
，下列结论正确的是（　　）
A．DE：BC=1：2
B．△ADE与△ABC的面积比为1：3
C．△ADE与△ABC的周长比为1：2
D．DE∥BC
组卷：2632引用：24难度：0.5
解析
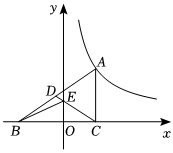8．如图，已知Rt△ABC中，∠ACB=90°，边BC在x轴上，点A落在反比例函数
y
=
8
x
的图象上，斜边AB上的中线CD交y轴于点E，则△BCE的面积是（　　）
A．4 B．
4
3
C．8 D．
8
3
组卷：4引用：3难度：0.5
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

三、解答题（共96分）

25．已知点O是线段AB的中点，点P是直线l上的任意一点，分别过点A和点B作直线l的垂线，垂足分别为点C和点D．我们定义垂足与中点之间的距离为“足中距”．

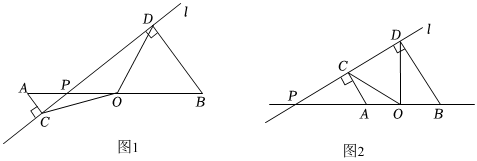
（1）[探究证明]如图1，当点P是线段AB上的任意一点时，“足中距”OC和OD存在怎样的数量关系，并给出证明过程．
（2）[拓展延伸]如图2，当点P是线段BA延长线上的任意一点时，若∠COD=60°，AC=2，BD=3，求CP的长．
组卷：21引用：2难度：0.5
解析
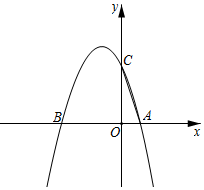26．如图，抛物线y=ax²+bx+c（a≠0）与x轴交于A、B两点，与y轴交于C点，AC=
10
，OB=OC=3OA．
（1）求抛物线的解析式；
（2）在第二象限内的抛物线上确定一点P，使四边形PBAC的面积最大，求出点P的坐标；
（3）在（2）的结论下，点M为x轴上一动点，抛物线上是否存在一点Q，使点P、B、M、Q为顶点的四边形是平行四边形，若存在，请直接写出Q点的坐标；若不存在，请说明理由．
组卷：2100引用：18难度：0.3
解析