当前位置：试卷中心 > 试卷详情

2023-2024学年广东省广州市越秀区执信中学高一（上）月考数学试卷（10月份）

发布：2024/9/9 9:0:8

一、单选题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.

1．命题“∃a∈R，ax²+1=0有实数解”的否定是（　　）
A．∀a∈R，ax²+1≠0有实数解 B．∃a∈R，ax²+1=0无实数解
C．∀a∈R，ax²+1=0无实数解 D．∃a∈R，ax²+1≠0有实数解
组卷：284引用：19难度：0.9
解析
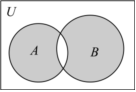2．已知全集U=R，集合A={x|x≥4或x≤0}，B={x|x＞4或x≤-2}，则图中阴影部分表示的集合为（　　）

A．（-2，0] B．[-2，0] C．[-2，0]∪{4} D．（-2，0]∪{4}
组卷：455引用：6难度：0.8
解析
3．已知a＞b＞c＞0，则（　　）
A．2a＜b+c B．a（b-c）＞b（a-c）
C．
1
a
-
c
＞
1
b
-
c
D．（a-c）³＞（b-c）³
组卷：160引用：11难度：0.7
解析
4．已知函数
f
（
x
）
=
x
2
+
x
,
x
＜
0
-
x
2
，
x
≥
0
，若f[f（a）]=2，则实数a的值为（　　）
A．-2 B．1 C．
2
D．2
组卷：50引用：2难度：0.5
解析
5．已知命题p：a∈D，命题q：∃x₀∈R，x₀²-ax₀-a≤-3，若p是q成立的必要不充分条件，则区间D为（　　）
A．（-∞，-6]∪[2，+∞） B．（-∞，-4）∪（0，+∞）
C．（-6，2） D．[-4，0]
组卷：204引用：7难度：0.6
解析
6．若关于x的不等式（a²-4）x²+（a+2）x-1≥0的解集不为空集，则实数a的取值范围为（　　）
A．（-2，
6
5
] B．[-2，
6
5
]
C．（-∞，-2）∪[
6
5
，+∞） D．（-∞，-2]∪[
6
5
，+∞）
组卷：414引用：8难度：0.8
解析
7．若对任意实数x＞0，y＞0，不等式
x
+
xy
≤
a
（
x
+
y
）
恒成立，则实数a的最小值为（　　）
A．
2
-
1
2
B．
2
-
1
C．
2
+
1
D．
2
+
1
2
组卷：503引用：12难度：0.6
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

四、解答题：本题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.

21．已知函数f（x）=x²+ax+2，a∈R．
（1）若不等式f（x）≤0的解集为[1，2]，求不等式f（x）≥1-x²的解集；
（2）若对于任意x∈[-1，1]，不等式f（x）≤2a（x-1）+4恒成立，求实数a的取值范围；
（3）已知g（x）=-x+m,当a=-3时，若对任意x₁∈[1，4]，总存在x₂∈（1，8），使f（x₁）=g（x₂）成立，求实数m的取值范围．
组卷：170引用：5难度：0.5
解析
22．设函数
f
（
x
）
=
1
a
x
,
0
≤
x
≤
a
1
1
-
a
（
1
-
x
）
，
a
＜
x
≤
1
，其中a为常数且a∈（0，1）．
新定义：若x₀满足f（f（x₀））=x₀，但f（x₀）≠x₀，则称x₀为f（x）的回旋点．
（1）当
a
=
1
2
时，分别求
f
（
f
（
1
3
）
）
和
f
（
f
（
4
5
）
）
的值；
（2）当x∈（a,1]时，求函数y=f（f（x））的解析式，并求出f（x）回旋点；
（3）证明函数f（x）在x∈[0，1]有且仅有两个回旋点，并求出回旋点x₁，x₂．
组卷：110引用：2难度：0.2
解析

0/60 进入组卷

0/20 进入试卷篮

布置作业 发布测评 反向细目表 平行组卷 下载答题卡 试卷分析 在线训练 收藏试卷

充值会员，资源免费下载

A．∀a∈R，ax²+1≠0有实数解	B．∃a∈R，ax²+1=0无实数解
C．∀a∈R，ax²+1=0无实数解	D．∃a∈R，ax²+1≠0有实数解

A．2a＜b+c	B．a（b-c）＞b（a-c）
C． 1 a - c ＞ 1 b - c	D．（a-c）³＞（b-c）³

A．（-∞，-6]∪[2，+∞）	B．（-∞，-4）∪（0，+∞）
C．（-6，2）	D．[-4，0]

A．（-2， 6 5 ]	B．[-2， 6 5 ]
C．（-∞，-2）∪[ 6 5 ，+∞）	D．（-∞，-2]∪[ 6 5 ，+∞）

2023-2024学年广东省广州市越秀区执信中学高一（上）月考数学试卷（10月份）

一、单选题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.

1．命题“∃a∈R，ax2+1=0有实数解”的否定是（ ）

2．已知全集U=R，集合A={x|x≥4或x≤0}，B={x|x＞4或x≤-2}，则图中阴影部分表示的集合为（ ）​

3．已知a＞b＞c＞0，则（ ）

4．已知函数f（x）=x2+x,x＜0-x2，x≥0，若f[f（a）]=2，则实数a的值为（ ）

5．已知命题p：a∈D，命题q：∃x0∈R，x02-ax0-a≤-3，若p是q成立的必要不充分条件，则区间D为（ ）

6．若关于x的不等式（a2-4）x2+（a+2）x-1≥0的解集不为空集，则实数a的取值范围为（ ）

7．若对任意实数x＞0，y＞0，不等式x+xy≤a（x+y）恒成立，则实数a的最小值为（ ）

四、解答题：本题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.

1．命题“∃a∈R，ax²+1=0有实数解”的否定是（　　）

2．已知全集U=R，集合A={x|x≥4或x≤0}，B={x|x＞4或x≤-2}，则图中阴影部分表示的集合为（　　）

3．已知a＞b＞c＞0，则（　　）

4．已知函数
f
（
x
）
=
x
2
+
x
,
x
＜
0
-
x
2
，
x
≥
0
，若f[f（a）]=2，则实数a的值为（　　）

5．已知命题p：a∈D，命题q：∃x₀∈R，x₀²-ax₀-a≤-3，若p是q成立的必要不充分条件，则区间D为（　　）

6．若关于x的不等式（a²-4）x²+（a+2）x-1≥0的解集不为空集，则实数a的取值范围为（　　）

7．若对任意实数x＞0，y＞0，不等式
x
+
xy
≤
a
（
x
+
y
）
恒成立，则实数a的最小值为（　　）