2023-2024学年河南省实验中学高三（上）开学数学试卷（理科）

一、选择题；本题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．

• 1．如果M={1，3，4}，N={2，4，5}，那么M∩N=（　　）

  A．∅

  B．{1，3}

  C．{4}

  D．{2，5}
  组卷：43引用：3难度：0.9

  解析

• 2．已知集合M={m|m=iⁿ，n∈N}，其中i为虚数单位，则下列元素属于集合M的是（　　）

  A．（1-i）（1+i）

  B． 1 - i 1 + i

  C． i 1 - i

  D．（1-i）2
  组卷：29引用：3难度：0.7

  解析

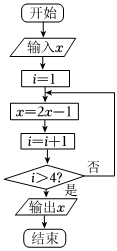• 3．《四元玉鉴》是一部辉煌的数学名著，是我国元朝著名数学家朱世杰的代表作，被视为中国筹算系统发展的顶峰，有些成果比欧洲早了400多年．其中有一首诗：“我有一壶酒，携着游春走，遇店添一倍，逢友饮一斗，店友经四处，没了半壶酒，借问此壶中，当原多少酒？”用程序框图表达如图所示，即最终输出的x=

  1

  2

  ，则开始输入的x值为（　　）

  A． 7 8

  B． 15 16

  C． 31 32

  D． 63 64
  组卷：36引用：3难度：0.7

  解析

• 4．用系统抽样法（按等距离的规则）要从160名学生中抽取容量为20的样本，将160名学生从1～160编号．按编号顺序平均分成20组（1～8号，9～16号，…，153～160号），若第16组应抽出的号码为125，则第一组中按此抽签方法确定的号码是（　　）

  A．7

  B．5

  C．4

  D．3
  组卷：51引用：15难度：0.9

  解析

• 5．已知某三棱锥的三视图如图所示，则该三棱锥的体积是（　　）

  A．1

  B． 3 2

  C．3

  D． 9 2
  组卷：212引用：4难度：0.7

  解析

• 6．已知

  sinx

  +

  cosx

  =

  3

  2

  ，则

  tanx

  +

  1

  tanx

  =（　　）

  A．-6

  B．-7

  C．-8

  D．-9
  组卷：791引用：6难度：0.8

  解析

• 7．如图，在直三棱柱ABD-A₁B₁D₁中，AD=BD=AA₁，∠DAB=45°，P为B₁D₁的中点，则直线BP与AD₁所成的角余弦值为（　　）

  A． 15 5

  B． 10 5

  C． 2 3

  D． 7 3
  组卷：54引用：2难度：0.6

  解析

三、解答题；本题共6个小题，共70分．解答应写出文字说明，证明过程或演算步骤．

• 22．在平面直角坐标系xOy中，曲线C₁的参数方程为

  x = 1 + cosα

  y = sinα

  （α为参数），以坐标原点O为极点，x轴非负半轴为极轴建立极坐标系，点A为曲线C₁上的动点，点B在线段OA的延长线上，且满足|OA|•|OB|=8，点B的轨迹为C₂．
  （1）求曲线C₁，C₂的极坐标方程；
  （2）设点M的极坐标为（2

  ，

  π

  2

  ），求△ABM面积的最小值．
  组卷：17引用：1难度：0.5

  解析

• 23．已知函数f（x）=|x-m|，m∈R
  （1）m=1时，求不等式f（x-2）+f（2x）＞4的解集；
  （2）若t＜0，求证：f（tx）≥tf（x）+f（tm）．
  组卷：87引用：4难度：0.7

  解析