2022-2023学年重庆市北碚区西南大学附中八年级（下）期末数学试卷

一、选择题（本大题共10个小题，每小题4分，共40分）在每个小题的下面，都给出了代号为A、B、C、D的四个答案，其中只有一个是正确的，请将答题卡上题号右侧正确答案所对应的方框涂黑.

• 1．下列四幅图案是四所大学校徽的主体标识，其中是中心对称图形的是（　　）

  A．

  B．

  C．

  D．
  组卷：34引用：1难度：0.7

  解析

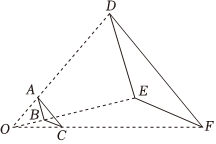• 2．如图，△ABC与△DEF是位似图形，位似比为1：4，若OA=2，则OD的长为（　　）
  ​

  A．4

  B．6

  C．8

  D．10
  组卷：103引用：1难度：0.7

  解析

• 3．下列调查，适合用普查方式的是（　　）

  A．调查重庆市初二年级学生的身高情况

  B．调查一批手机的使用寿命情况

  C．调查我校初二1班学生每周体锻时间

  D．调查今年“6•18”我市市民在某宝的消费情况
  组卷：36引用：2难度：0.7

  解析

• 4．将抛物线y=3x²+2向右平移1个单位，再向上平移3个单位后所得到的抛物线解析式为（　　）

  A．y=3（x+1）2+5	B．y=3（x-1）2+5
  C．y=3（x+1）2-1	D．y=3（x-1）2-1
  组卷：379引用：4难度：0.5

  解析

• 5．在同一平面直角坐标系中，函数y=kx+k与y=

  k

  x

  （k≠0）的图象可能是（　　）

  A．

  B．

  C．

  D．
  组卷：1704引用：10难度：0.6

  解析

• 6．宾馆有50间房供游客居住，当每间房每天定价为180元时，宾馆会住满；当每间房每天的定价每增加10元时，就会空闲一间房．如果有游客居住，宾馆需对居住的每间房每天支出20元的费用．当房价定为多少元时，宾馆当天的利润为10890元？设房价比定价180元增加x元，则有（　　）

  A．（x-20）（50- x - 180 10 ）=10890

  B．x（50- x - 180 10 ）-50×20=10890

  C．（180+x-20）（50- x 10 ）=10890

  D．（x+180）（50- x 10 ）-50×20=10890
  组卷：1494引用：8难度：0.7

  解析

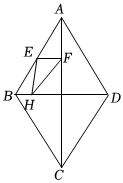• 7．如图，已知菱形ABCD的对角线AC，BD相交于点O，AC=8，BD=6，点E、F分别为AB、AO的中点，点H为BD上的动点，连接FH，EH，则FH+EH的最小值为（　　）

  A． 13

  B．5

  C． 55 2

  D． 73 2
  组卷：175引用：1难度：0.5

  解析

• 8．当a-1≤x≤a时，二次函数y=x²-4x+3的最小值为8，则a的值为（　　）

  A．-1 或5

  B．0或6

  C．-1或6

  D．0或5
  组卷：1321引用：1难度：0.7

  解析

三、解答题（本大题共8个小题，19题8分，20～26每小题8分，共78分）解答时每小题必须给出必要的演算过程或推理步骤，画出必要的图形（包括辅助线），请将解答过程书写在答题卡中对应的位置上.

• 25．若直线

  y

  =

  1

  2

  x

  -

  5

  2

  与y轴交于点A，与x轴交于点B，二次函数y=ax²+bx+c的图象经过点A，点B，且抛物线的对称轴为直线x=2．
  （1）求二次函数的解析式；
  （2）若点P为直线AB下方抛物线上一点，过点P作直线AB的垂线，垂足为E，作PF∥y轴交直线AB于点F，求△PEF周长的最大值及此时点P的坐标；
  （3）将抛物线沿射线AB方向平移

  5

  个单位长度得到新抛物线y′，Q是新抛物线与原抛物线的交点，N是原抛物线对称轴上一动点，在平面内确定一点M，使得以M，N，B，Q为顶点的四边形是以BN为边的菱形，请写出所有符合条件的点M的坐标，并写出求解点M坐标的其中一种情况的过程．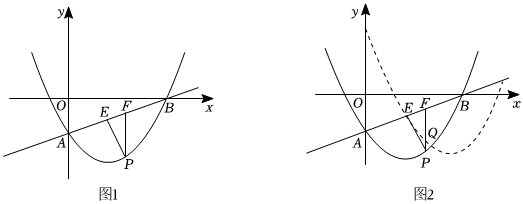
  
  组卷：297引用：1难度：0.2

  解析

• 26．在△ABC中，∠ABC=45°，∠CAB=30°，BC=6，E是线段AB上一动点，连接CE．
  
  （1）如图1，若AE=AC，求△AEC的面积；
  （2）如图2，若CE=CB，将线段CA绕C逆时针旋转90°得到线段CF，连接BF．若点G是线段EB的中点，过点G作GP∥EC交BC于点P，交AF于点H，证明AH=HF；
  （3）如图3，将△CEB沿CE翻折至△CEB′，连接AB′．D是线段AC上的点，且AD=BE，直接写出当CE+BD取得最小值时AB′的长度．
  组卷：706引用：5难度：0.1

  解析