2023-2024学年江苏省南通市崇川区启秀中学八年级（上）第一次月考数学试卷

一、选择题（共10小题，每小题3分，共30分）

• 1．下列说法正确的是（　　）

  A．面积相等的两个三角形全等

  B．周长相等的两个三角形全等

  C．形状相同的两个三角形全等

  D．能够完全重合的两个三角形全等
  组卷：101引用：3难度：0.7

  解析

• 2．下列计算正确的是（　　）

  A．（3a）2=6a2

  B．（a2）3=a5

  C．a6÷a2=a3

  D．a2•a=a3
  组卷：128引用：3难度：0.7

  解析

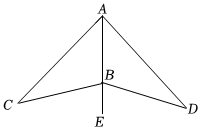• 3．如图，在△ABC和△ABD中，∠CAB=∠DAB，点A，B，E在同一条直线上，则添加以下条件，仍然不能判定△ABC≌△ABD的是（　　）

  A．∠C=∠D

  B．∠CBE=∠DBE

  C．BC=BD

  D．AC=AD
  组卷：188引用：6难度：0.6

  解析

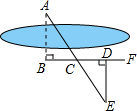• 4．如图，要测量河两岸相对的两点A、B的距离，先在AB的垂线BF上取两点C、D，使BC=CD，再作出BF的垂线DE，使点A、C、E在同一条直线上（如图），可以说明△ABC≌△EDC，得AB=DE，因此测得DE的长就是AB的长，判定△ABC≌△EDC，最恰当的理由是（　　）

  A．SAS

  B．HL

  C．SSS

  D．ASA
  组卷：3192引用：37难度：0.5

  解析

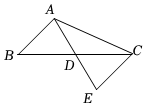• 5．如图，AD是△ABC的中线，CE∥AB交AD的延长线于点E，AB=5，AC=7，则AD的取值不可能是（　　）

  A．3

  B．4

  C．5

  D．6
  组卷：338引用：2难度：0.5

  解析

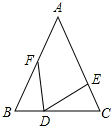• 6．如图，在△ABC中，∠B=∠C，BF=CD，BD=CE，∠FDE=50°，则∠A的度数是（　　）

  A．50°

  B．60°

  C．70°

  D．80°
  组卷：657引用：7难度：0.6

  解析

• 7．若6⁵+6⁵+6⁵+6⁵+6⁵+6⁵=36ⁿ，则n的值为（　　）

  A．10

  B．6

  C．5

  D．3
  组卷：352引用：4难度：0.5

  解析

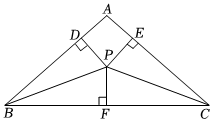• 8．如图，点P是△ABC内部的一点，点P到三边AB，AC，BC的距离PD=PE=PF，∠BPC=130°，则∠BAC的度数为（　　）

  A．65°

  B．80°

  C．100°

  D．70°
  组卷：565引用：8难度：0.5

  解析

三、解答题（8题，共90分）

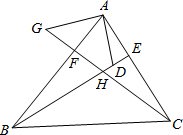• 25．如图：在△ABC中，BE、CF分别是AC、AB两边上的高，在BE上截取BD=AC，在CF的延长线上截取CG=AB，连结AD、AG．
  （1）求证：∠ABE=∠ACG；
  （2）试判：AG与AD的关系？并说明理由．
  组卷：1872引用：6难度：0.5

  解析

• 26．在△ABC中，AB=AC，点D是射线CB上的一动点（不与点B、C重合），以AD为一边在AD的右侧作△ADE，使AD=AE，∠DAE=∠BAC，连接CE．
  （1）如图1，当点D在线段CB上，且∠BAC=90°时，那么∠DCE=

  度；
  （2）设∠BAC=α，∠DCE=β．
  ①如图2，当点D在线段CB上，∠BAC≠90°时，请你探究α与β之间的数量关系，并证明你的结论；
  ②如图3，当点D在线段CB的延长线上，∠BAC≠90°时，请将图3补充完整，写出此时α与β之间的数量关系并证明．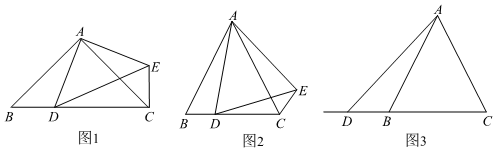
  
  组卷：1690引用：18难度：0.6

  解析