当前位置：试卷中心 > 试卷详情

2023年江苏省常州市新北实验中学中考数学二模试卷

发布：2024/9/27 1:0:4

一、选择题(本大题共18小题,每小题2分,共16分,在每小题所给的四个选项中,只有一项是正确的,请把答案直接填写在答题卡相应的位罩上)

1．-2的绝对值是（　　）
A．2 B．-2 C．
1
2
D．-
1
2
组卷：6445引用：782难度：0.9
解析
2．若代数式
x
有意义，则实数x的取值范围是（　　）
A．x≠1 B．x≥0 C．x＞0 D．x≥0且x≠1
组卷：93引用：3难度：0.9
解析
3．下列各式计算正确的是（　　）
A．m+m=m² B．2m-m=2 C．（-m）³=m³ D．m•3m³=3m⁴
组卷：135引用：1难度：0.9
解析
4．一个几何体的主视图是圆，这个几何体可能是（　　）
A．三棱柱 B．正方体 C．圆柱 D．三棱锥
组卷：65引用：1难度：0.7
解析
5．著名数学家、教育家华罗庚出生地是常州哪个地区？（　　）
A．金坛区 B．武进区 C．溧阳市 D．天宁区
组卷：161引用：2难度：0.9
解析
6．多边形的每个内角均为120°，则这个多边形的边数是（　　）
A．4 B．5 C．6 D．8
组卷：616引用：10难度：0.9
解析
7．下面四组a,b的值，能说明命题“若a²＞b²，则a＞b”是假命题的是（　　）
A．a=2，b=1 B．a=-2，b=1 C．a=2，b=-1 D．a=3，b=-2
组卷：246引用：3难度：0.7
解析
8．如图，菱形ABCD的对角线AC，BD交于点P，且AC过原点O，AB∥x轴，点C的坐标为（6，3），反比例函数y=
k
x
的图象经过A，P两点，则k的值是（　　）
A．4 B．3 C．2 D．1
组卷：2882引用：11难度：0.4
解析
9．-27的立方根是
．
组卷：181引用：3难度：0.7
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

三、解答题(本大题共10小题,共84分,请在答题卡指定区域内作答,如无特殊说明,解答应写出文字说明、演算步骤或推理过程)

27．阅读理解早在我国南宋时期，著名的数学家秦九韶在其著作《数书九章》中，提出了“三斜求积术”，即已知三角形三边长求三角形面积的公式，后人称之为“秦九韶公式”，其求法是：若将三角形的三条边分别称为小斜（记为a）、中斜（记为b）和大斜（记为c），以小斜幂并大斜幂减中斜幂，余半之，自乘于上，以小斜幂乘大斜幂减上，余四约之，为实：一为从隔，开平方得积．若把以上这段文字写成公式即为
1
4
[
a
2
c
2
-
（
a
2
+
c
2
-
b
2
2
）
2
]
，（a＜b＜c），其中a、b、c为2三角形三边的长．请用此公式解决下列问题：
（1）如图，已知图中3个正方形的面积分别为2，1，4，求△ABC的面积．
深入探究
古希腊数学家海伦写了一本《测量仪论》，上面记载一个计算三角形面积的公式，即海伦公式：三角形面积S=
p
（
p
-
a
）
（
p
-
b
）
（
p
-
c
）
，其中a、b、c为三角形三边长，p=
a
+
b
+
c
2
，
（2）请你用秦九韶公式证明海伦公式．
灵活应用
结合上面学习的知识解决以下问题：
（3）已知三角形三边长分别为5，6，7，求这个三角形的内切圆半径．
组卷：227引用：1难度：0.2
解析
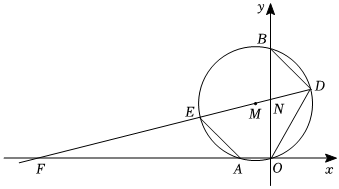28．如图，在平面直角坐标系xOy中，点A、点B的坐标分别为（-2，0）、（0，8）．经过A、B、O三点的圆的圆心为M，过点M的直线与⊙M的公共点是D、E，与x轴交于点F，与y轴交于点N，连接AE、OD、BD．已知∠ODF=45°．
（1）⊙M的直径为
，点M的坐标为
；
（2）求直线DF所对应的函数表达式；
（3）若P是线段AF上的动点，∠PEA与△BDO的一个内角相等，求OP的长度．
组卷：363引用：1难度：0.1
解析