北师大新版八年级上册《1.1 探索勾股定理（验证并应用勾股定理）》2023年同步练习卷

一、选择题

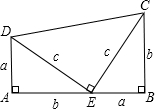• 1．历史上对勾股定理的一种证法采用了下列图形：其中两个全等的直角三角形边AE、EB在一条直线上．证明中用到的面积相等关系是（　　）

  A．S△EDA=S△CEB

  B．S△EDA+S△CEB=S△CDE

  C．S四边形CDAE=S四边形CDEB

  D．S△EDA+S△CDE+S△CEB=S四边形ABCD
  组卷：1036引用：15难度：0.7

  解析

• 2．下面图形能够验证勾股定理的有（　　）
  

  A．4个

  B．3个

  C．2个

  D．1个
  组卷：1628引用：6难度：0.6

  解析

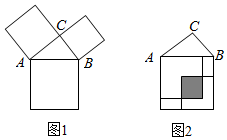• 3．勾股定理是人类最伟大的科学发现之一，在我国古算书《周髀算经》中早有记载．如图1，以直角三角形的各边为边分别向外作正方形，再把较小的两个正方形按图2的方式放入最大的正方形内，若图2中阴影部分的面积为4，且AC+BC=7，则AB的长为（　　）

  A．5

  B．9

  C． 29

  D． 37
  组卷：960引用：7难度：0.4

  解析

三、解答题

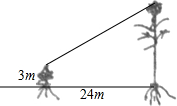• 8．有一只喜鹊在一棵3m高的小树上觅食，它的巢筑在距离该树24m远的一棵大树上，大树高14m,且巢离树顶部1m,当它听到巢中幼鸟的叫声，立即赶过去，如果它飞行的速度为5m/s,那它至少需要多少时间才能赶回巢中？（画出符合题意的几何图形，并求解）
  组卷：563引用：4难度：0.5

  解析

• 9．△ABC中，BC=a,AC=b,AB=c.若∠C=90°，如图1，根据勾股定理，则a²+b²=c²．若△ABC不是直角三角形，如图2和图3，请你类比勾股定理，试猜想a²+b²与c²的关系，并证明你的结论．
  
  组卷：3988引用：45难度：0.3

  解析