2023-2024学年北京市海淀区清华附中上地学校九年级(上)开学数学试卷
发布:2024/8/6 8:0:9
一、选择题(共24分,每题3分)
-
 1.正比例函数y=kx(k≠0)的图象如图所示,则一次函数y=x-k的图象大致是( )组卷:345引用:5难度:0.7
1.正比例函数y=kx(k≠0)的图象如图所示,则一次函数y=x-k的图象大致是( )组卷:345引用:5难度:0.7 -
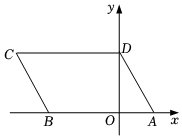 2.如图,平行四边形ABCD的顶点A,B,D的坐标分别是(1,0),(-2,0),(0,2),则顶点C的坐标是( )组卷:280引用:6难度:0.7
2.如图,平行四边形ABCD的顶点A,B,D的坐标分别是(1,0),(-2,0),(0,2),则顶点C的坐标是( )组卷:280引用:6难度:0.7 -
3.抛物线y=x2向上平移2个单位,所得抛物线的解析式是( )
组卷:329引用:5难度:0.8 -
4.用配方法解方程x2+4x+1=0,下列变形正确的是( )
组卷:373引用:12难度:0.6 -
5.已知y=x2+(m-1)x+1,当0≤x≤5且x为整数时,y随x的增大而减小,则m的取值范围是( )
组卷:332引用:7难度:0.5 -
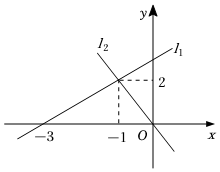 6.直线l1:y1=ax+b与l2:y2=mx的图象如图所示,则关于x的不等式mx<ax+b的解集为( )组卷:390引用:3难度:0.5
6.直线l1:y1=ax+b与l2:y2=mx的图象如图所示,则关于x的不等式mx<ax+b的解集为( )组卷:390引用:3难度:0.5 -
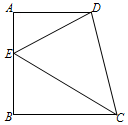 7.如图,在四边形ABCD中,∠A=∠B=90°,AB=BC=4,AD=3,E是边AB上一点,且∠DCE=45°,则DE的长度是( )组卷:3102引用:8难度:0.4
7.如图,在四边形ABCD中,∠A=∠B=90°,AB=BC=4,AD=3,E是边AB上一点,且∠DCE=45°,则DE的长度是( )组卷:3102引用:8难度:0.4 -
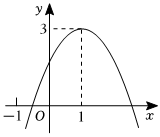 8.二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论①abc<0;②2a+b>0;③b2-4ac>0;④3a+c<0;⑤ax2+bx+c-3=0有两个不相等的实数根.其中正确的个数是( )组卷:781引用:6难度:0.6
8.二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论①abc<0;②2a+b>0;③b2-4ac>0;④3a+c<0;⑤ax2+bx+c-3=0有两个不相等的实数根.其中正确的个数是( )组卷:781引用:6难度:0.6
三、解答题(共52分,17题共8分,18~22每题5分,23~24每题6分,25题7分)
-
24.△ABC是等边三角形,点D在BC上,点E,F分别在射线AB,AC上,且DA=DE=DF.
(1)如图1,当点D是BC的中点时,则∠EDF=°;
(2)如图2,点D在BC上运动(不与点B,C重合).
①判断∠EDF的大小是否发生改变,并说明理由;
②点D关于射线AC的对称点为点G,连接BG,CG,CE.
依题意补全图形,判断四边形BECG的形状,并证明你的结论.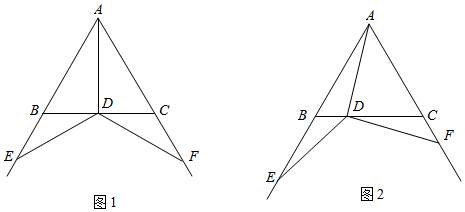 组卷:324引用:3难度:0.4
组卷:324引用:3难度:0.4 -
 25.对于平面直角坐标系xOy中的点P,Q和图形G,给出如下定义:点P,Q都在图形G上,且将点P的横坐标与纵坐标互换后得到点Q,则称点P,Q是图形G的一对“关联点”.例如,点P(3,2)和点Q(2,3)是函数的一对关联点.y=6x
25.对于平面直角坐标系xOy中的点P,Q和图形G,给出如下定义:点P,Q都在图形G上,且将点P的横坐标与纵坐标互换后得到点Q,则称点P,Q是图形G的一对“关联点”.例如,点P(3,2)和点Q(2,3)是函数的一对关联点.y=6x
(1)请写出一次函数y=-x+3的图象上的一对关联点的坐标:;
(2)抛物线y=x2+bx+c的对称轴为直线x=1,与y轴交于点C(0,-1).点A,B是抛物线y=x2+bx+c的一对关联点,直线AB与x轴交于点D(1,0).求A,B两点坐标.组卷:71引用:1难度:0.5


