2022-2023学年贵州省铜仁十一中九年级（上）期中数学试卷

一、单选题（共10小题，每题4分，共40分）

• 1．下列函数不是反比例函数的是（　　）

  A．y=3x-1

  B．y=- x 3

  C．xy=5

  D．y= 1 2 x
  组卷：2533引用：30难度：0.9

  解析

• 2．在比例尺为1：1000000的地图上，甲、乙两地图距是2cm,它的实际长度约为（　　）

  A．200km

  B．2km

  C．200000km

  D．20km
  组卷：11引用：2难度：0.5

  解析

• 3．在Rt△ABC中，∠C=90°，AC=5，AB=13，则sinA的值为（　　）

  A． 5 12

  B． 5 13

  C． 12 13

  D． 13 12
  组卷：270引用：6难度：0.9

  解析

• 4．用配方法解一元二次方程x²-8x+7=0，方程可变形为（　　）

  A．（x+4）2=9

  B．（x-4）2=9

  C．（x-8）2=16

  D．（x+8）2=57
  组卷：1396引用：30难度：0.9

  解析

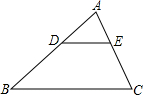• 5．如图所示：△ABC中，DE∥BC，AD=5，BD=10，AE=3．则CE的值为（　　）

  A．9

  B．6

  C．3

  D．4
  组卷：657引用：32难度：0.9

  解析

• 6．某校九年级进行了三次数学考试，甲、乙、丙、丁四名同学成绩的平均数

  x

  _甲=

  x

  _乙=

  x

  _丙=

  x

  _丁=111.5，方差S²分别为S_甲²=3.6，S_乙²=6，S_丙²=10，S_丁²=3.2，那么这四名同学数学成绩最稳定的是（　　）

  A．甲

  B．乙

  C．丙

  D．丁
  组卷：2引用：1难度：0.5

  解析

• 7．定义运算：m⊕n=n²-mn+1．例如：1⊕2=2²-1×2+1=3，则方程1⊕x=0的根的情况为（　　）

  A．无实数根	B．只有一个实数根
  C．有两个相等的实数根	D．有两个不相等的实数根
  组卷：387引用：8难度：0.7

  解析

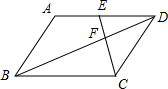• 8．如图，在平行四边形ABCD中，E为AD的中点，△BCF的面积为4，则△DEF的面积为（　　）

  A．1

  B．2

  C．3

  D．4
  组卷：184引用：7难度：0.9

  解析

三、解答题（共86分）

• 23．阅读材料，解答问题：
  【材料1】
  为了解方程（x²）²-13x²+36=0，如果我们把x²看作一个整体，然后设y=x²，则原方程可化为y²-13y+36=0，经过运算，原方程的解为x_1，2=±2，x_3，4=±3．我们把以上这种解决问题的方法通常叫做换元法．
  【材料2】
  已知实数m,n满足m²-m-1=0，n²-n-1=0，且m≠n,显然m,n是方程x²-x-1=0的两个不相等的实数根，由韦达定理可知m+n=1，mn=-1．
  根据上述材料，解决以下问题：
  （1）直接应用：
  方程x⁴-5x²+6=0的解为

  ；
  （2）间接应用：
  已知实数a,b满足：2a⁴-7a²+1=0，2b⁴-7b²+1=0且a≠b,求a⁴+b⁴的值．
  组卷：341引用：5难度：0.6

  解析

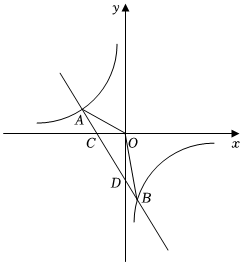• 24．如图，直线y=k₁x+b与双曲线y=

  k

  2

  x

  交于A，B两点，已知点A的横坐标为-3，点B的纵坐标为-3，直线AB与x轴交于点C，与y轴交于点D（0，-2），tan∠AOC=

  1

  3

  ．
  （1）求双曲线和直线AB的解析式；
  （2）若点P是第二象限内反比例函数图象上的一点，△OCP的面积是△ODB的面积的3倍，求点P的坐标；
  （3）若点E在x轴的负半轴上，是否存在以点E，C，D为顶点构成的三角形与△ODB相似？若存在，求出点E的坐标；若不存在，请说明理由．
  组卷：1405引用：5难度：0.4

  解析