2022-2023学年广西北海市高一（下）期末数学试卷

一、单项选择题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.

• 1．下列各角中，与2183°角终边相同的是（　　）

  A．-23°

  B．23°

  C．-47°

  D．47°
  组卷：194引用：2难度：0.8

  解析

• 2．已知互不重合的直线m,n,互不重合的平面 α，β，γ，下列命题错误的是（　　）

  A．若α∥β，β∥γ，则α∥γ	B．若α∥β，β⊥γ，则α⊥γ
  C．若α∥β，m∥α，则m∥β	D．若α∥β，n⊂α，则n∥β
  组卷：210引用：6难度：0.7

  解析

• 3．已知复数z满足

  z

  +

  2

  z

  =

  3

  +

  4

  i

  （i是虚数单位），则z=（　　）

  A．1-4i

  B．6-4i

  C．6-2i

  D．3-2i
  组卷：72引用：14难度：0.7

  解析

• 4．已知两个单位向量

  a

  ，

  b

  的夹角为120°，若

  3

  a

  -

  b

  +

  c

  =

  0

  ，则

  |

  c

  |

  =（　　）

  A． 7

  B．13

  C．7

  D． 13
  组卷：50引用：1难度：0.7

  解析

• 5．为了得到函数

  f

  （

  x

  ）

  =

  1

  2

  cos

  （

  x

  +

  π

  3

  ）

  的图象，只需把曲线g（x）=cosx上所有的点（　　）

  A．向左平移 π 3 个单位，再把纵坐标伸长到原来的2倍

  B．向右平移 π 3 个单位，再把纵坐标伸长到原来的2倍

  C．向左平移 π 3 个单位，再把纵坐标缩短到原来的 1 2

  D．向右平移 π 3 个单位，再把纵坐标缩短到原来的 1 2
  组卷：147引用：2难度：0.5

  解析

• 6．著名的古希腊数学家阿基米德一生最为满意的一个数学发现就是“圆柱容球”定理：把一个球放在一个圆柱形的容器中，如果盖上容器的上盖后，球恰好与圆柱的上、下底面和侧面相切（该球也被称为圆柱的内切球），那么此时圆柱的内切球体积与圆柱体积之比为定值，则该定值为（　　）

  A． 1 2

  B． 1 3

  C． 3 4

  D． 2 3
  组卷：113引用：5难度：0.7

  解析

• 7．若圆台的高是

  2

  3

  ，一个底面半径是另一个底面半径的2倍，母线与下底面所成角的大小为60°，则这个圆台的侧面积是（　　）

  A．24π

  B． 8 3 π

  C． 9 3 π

  D．27π
  组卷：59引用：2难度：0.8

  解析

四、解答题：本题共6小题，共70分.解答应写出必要的文字说明、证明过程及演算步骤.

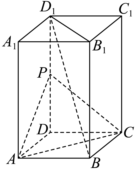• 21．如图，四棱柱ABCD-A₁B₁C₁D₁的底面ABCD是菱形，AA₁⊥平面ABCD，AB=1，AA₁=2，∠BAD=60°，点P为DD₁的中点．
  （1）求证：直线BD₁∥平面PAC；
  （2）求二面角B₁-AC-P的余弦值．
  
  组卷：344引用：6难度：0.5

  解析

• 22．已知函数f（x）=sinx+cosx+asin2x（a∈R）．
  （1）若a=4，求f（x）的最大值；
  （2）若f（x）在[-π，0]上恰有3个零点，求实数a的取值范围．
  组卷：43引用：1难度：0.5

  解析