当前位置：试卷中心 > 试卷详情

2023-2024学年广西来宾市八年级（上）期中数学试卷

发布：2024/10/2 17:0:2

一、选择题（本大题共12小题，每小题3分，满分36分.在每个小题给出的四个选项中，只有一项是正确的，每小题选对得3分，选错、不选或多选均得0分）

1．若分式
x
-
2
3
x
-
1
的值为0，则x的值是（　　）
A．-2 B．0 C．2 D．
1
3
组卷：173引用：3难度：0.8
解析
2．下列长度的三条线段，能组成三角形的是（　　）
A．1，2，3 B．2，2，4 C．3，4，5 D．3，6，10
组卷：47引用：3难度：0.7
解析
3．如图，生活中都把自行车的几根梁做成三角形的支架，这是利用三角形的（　　）
A．全等形 B．稳定性 C．灵活性 D．对称性
组卷：3680引用：50难度：0.8
解析
4．某同学把一块三角形的玻璃打碎成了3块，现在要到玻璃店去配一块完全一样的玻璃，那么最省事方法是（　　）
A．带①去 B．带②去 C．带③去 D．①②③都带去
组卷：5174引用：169难度：0.9
解析
5．下面四个图形中，线段AD是△ABC的高的是（　　）
A． B． C． D．
组卷：1372引用：8难度：0.8
解析
6．对于分式
x
2
+
y
2
2
x
+
y
，若将x,y的值都扩大到原来的3倍，则分式的值（　　）
A．扩大到原来的3倍 B．扩大到原来的9倍
C．不变 D．无法确定
组卷：303引用：5难度：0.7
解析

7．小明和小亮解答“解分式方程：
2
x
+
3
x
=
1
-
x
-
1
x
”的过程如下，对他们的解答过程有以下判断，判断正确的是（　　）

小明的解法：
解：去分母，得2x+3=1-（x-1），①
去括号，得2x+3=1-x+1，②
移项，得2x+x=1+1-3，③
合并同类项，得3x=-1，④
系数化为1，得x=-
1
3
，⑤
经检验x=-
1
3
是原分式方程的解．⑥ 小亮的解法：
解：去分母，得2x+3=x-（x-1），①
去括号，得2x+3=x-x+1，②
移项，得2x=-3+1，③
合并同类项，得2x=-2，④
系数化为1，得x=-1，⑤
经检验x=-1是原分式方程的解．⑥

A．小明正确，小亮错误	B．小明错误，小亮正确
C．两人都正确	D．两人都错误

组卷：226引用：3难度：0.7

解析

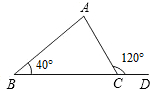8．如图，在△ABC中，D是BC延长线上一点，∠B=40°，∠ACD=120°，则∠A等于（　　）
A．60° B．70° C．80° D．90°
组卷：2594引用：192难度：0.9
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

三、解答题（本大题共8小题，满分72分.解答时应写出必要的文字说明、演算步骤或推理过程.请将解答写在答题卡中相应的区域内，画图或作辅助线时使用铅笔画出，确定后必须使用黑色字迹的签字笔描黑.在草稿纸、试卷上答题无效）

25．如图所示，已知BD为△ABC的角平分线，CD为△ABC外角∠ACE的平分线，且与BD交于点D；
（1）若∠ABC=60°，∠DCE=70°，则∠D=

°；
（2）若∠ABC=70°，∠A=80°，则∠D=

°；
（3）当∠ABC和∠ACB在变化，而∠A始终保持不变，则∠D是否发生变化？为什么？由此你能得出什么结论？（用含∠A的式子表示∠D）
组卷：276引用：3难度：0.3
解析
26．综合与实践
八年级二班数学兴趣小组在一次活动中进行了探究实验活动，请你和他们一起探究吧．
【发现问题】他们在探究实验活动中遇到了下面的问题：如图1，AD是△ABC的中线，若AB=5，AC=3，求AD的长的取值范围．
【探究方法】他们通过探究发现，延长AD至点E，使ED=AD，连接BE．可以证出△ADC≌△EDB，利用全等三角形的性质可将已知的边长与AD转化到△ABE中，进而求出AD的长的取值范围．
【方法小结】从上面的思路可以看出，解决问题的关键是将中线AD延长一倍，构造出全等三角形，我们把这种方法叫做“倍长中线法”．
（1）请你利用上面解答问题的思路方法，写出求解AD的长的取值范围的过程．
【问题解决】
（2）如图2，CB是△AEC的中线，CD是△ABC的中线，且AB=AC，下列有四个选项：
A．∠ACD=∠BCD
B．CE=2CD
C．∠BCD=∠BCE
D．CD=CB
直接写出所有正确的选项：
．
【问题拓展】
（3）如图3，在△ABO和△CDO中，OA=OB，OC=OD，∠AOB与∠COD互补，连接AC，BD，取BD的中点E，连接OE，求证：
OE
=
1
2
AC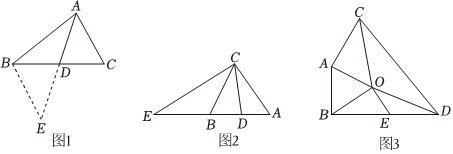
．
组卷：263引用：2难度：0.2
解析