2022-2023学年山西省大同市阳高四中高二(下)期末数学试卷
发布:2024/6/3 8:0:1
一、选择题(本大题共12道小题,每小题5分,共计60分。在每小题给出的四个选项中,只有一项是符合题目要求的.)
-
1.i为虚数单位,则
=( )i2i4+i组卷:80引用:5难度:0.8 -
2.已知函数
在点x=x0处的切线的倾斜角是f(x)=x,则x0的值为( )π4组卷:335引用:5难度:0.8 -
3.已知双曲线
的离心率C:x2a2-y2b2=1,且其右焦点为F(4,0),则双曲线C的方程为( )e=43组卷:63引用:5难度:0.7 -
4.曲线y=x2和曲线y2=x围成的图形面积是( )
组卷:208引用:24难度:0.9 -
5.已知椭圆
的左、右焦点分别为F1,F2,过C的左焦点作一条直线与椭圆相交于A,B两点,若C:x2a2+y2b2=1(a>b>0)且BF1=F1H=HA,则C的离心率为( )HF2•AB=0组卷:133引用:2难度:0.5 -
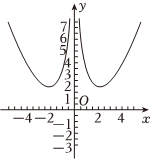 6.已知函数y=f(x)的大致图象如图所示,则f(x)的解析式可能为( )组卷:64引用:3难度:0.7
6.已知函数y=f(x)的大致图象如图所示,则f(x)的解析式可能为( )组卷:64引用:3难度:0.7 -
7.若x,y满足约束条件
则z=x2+y2的最大值是( )2x-y≥0,x+2y-5≥0,3x+y-10≤0,组卷:54引用:5难度:0.7
三、解答题(本大题共6小题,第17题10分,其余每题12分,共70分)
-
21.已知复数z=a+bi(a,b∈R).
(1)若复数z在复平面内对应的点位于实轴上方(不包括实轴),求a,b满足的条件;
(2)若(a+2)-2ai=-3b+(b-1)i,求a,b的值.组卷:25引用:2难度:0.8 -
22.某地经过多年的环境治理,已将荒山改造成了绿水青山.为估计一林区某种树木的材积量,随机选取了10棵这种树木,测量每棵树的根部横截面积(单位:m2)和材积量(单位:m3),得到如下数据:
由散点图知根部横截面积与材积量线性相关,并计算得样本号i 1 2 3 4 5 6 7 8 9 10 总和 根部横截面积xi 0.04 0.06 0.04 0.08 0.08 0.05 0.05 0.07 0.07 0.06 0.6 材积量yi 0.25 0.40 0.22 0.54 0.51 0.34 0.36 0.46 0.42 0.40 3.9 .10∑i=1x2i=0.038,10∑i=1xiyi=0.2474
(1)估计该林区这种树木平均一棵的根部横截面积与平均一棵的材积量;
(2)求该林区这种树木的根部横截面积与材积量的回归直线方程;
(3)现测量了该林区2500棵这种树木的根部横截面积,并得到这些树木的根部横截面积总和为.利用(2)中所求的回归直线方程,估计这些树木的总材积量.2500∑i=1xi=153m2
附:回归直线方程的斜率,截距̂b=n∑i=1xiyi-nxyn∑i=1x2i-nx2.̂a=y-̂bx组卷:19引用:2难度:0.6


