2022-2023学年广东省梅州市丰顺县东留中学九年级（上）月考数学试卷（9月份）

一、选择题（共10题，共30分）

• 1．方程（x-2）²-1=0的解是（　　）

  A．x1=1，x2=2	B．x1=1，x2=3
  C．x1=x2=3	D．x1=-1，x2=-3
  组卷：5引用：2难度：0.6

  解析

• 2．下列方程中是一元二次方程的是（　　）

  A．ax2+bx+c=0	B．x2-2xy+y2=0
  C．x2-x=0	D．x2+ 1 x 2 =1
  组卷：190引用：3难度：0.8

  解析

• 3．一元二次方程（1-k）x²-2x-1=0有两个不相等的实数根，则k的取值范围是（　　）

  A．k＜2且k≠1

  B．k＞2且k≠1

  C．k＞2

  D．k＜2
  组卷：156引用：5难度：0.9

  解析

• 4．如图，E、F分别是正方形ABCD的边CD，AD上的点，且CE=DF，AE，BF相交于点O，下列结论①AE=BF；②AE⊥BF；③AO=OE；④S_△AOB=S_{四边形DEOF}中，正确结论的个数为（　　）

  A．4个

  B．3个

  C．2个

  D．1个
  组卷：3043引用：25难度：0.7

  解析

• 5．关于x的一元二次方程kx²-4x+1=0有实数根，则k的取值范围是（　　）

  A．k≥-4

  B．k≥-4且k≠0

  C．k≤4

  D．k≤4且k≠0
  组卷：518引用：13难度：0.9

  解析

• 6．如图，点P是菱形ABCD边上的动点，它从点A出发沿A→B→C→D路径匀速运动到点D，设△PAD的面积为y,P点的运动时间为x,则y关于x的函数图象大致为（　　）

  A．

  B．

  C．

  D．
  组卷：2105引用：17难度：0.7

  解析

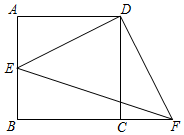• 7．如图，在正方形ABCD中，E为AB中点，连接DE，过点D作DF⊥DE交BC的延长线于点F，连接EF．若AE=1，则EF的值为（　　）

  A．3

  B． 10

  C．2 3

  D．4
  组卷：1874引用：12难度：0.8

  解析

• 8．函数y=kx+b的图象如图所示，则关于x的一元二次方程x²+bx+k-1=0的根的情况是（　　）

  A．没有实数根	B．有两个相等的实数根
  C．有两个不相等的实数根	D．无法确定
  组卷：618引用：5难度：0.6

  解析

三、解答题（共8小题，满分62分）

• 24．阅读下面材料：
  小明遇到这样一个问题：如图1，在矩形ABCD中，对角线AC、BD相交于点O，且∠AOB=60°，点E、F、G分别是OB、OC、AD的中点，连接所EF、FG、GE．
  求证：△EFG是等边三角形．
  小明经探究发现，连接AE、DF（如图2），从而可证AE⊥BD，DF⊥AC，使问题得到解决．
  （1）请你按照小明的探究思路，完成他的证明过程；
  参考小明思考问题的方法或用其他的方法，解决下面的问题：
  （2）如图3，在四边形ABCD中，AB=AO，DC=DO，对角线AC、BD相交于点O，且∠AOB=n°（0＜n＜90），点E、F、G分别是OB、OC、AD的中点，连接EF、FG、GE．
  ①否存在与GE相等的线段？若存在，请找出并证明；若不存在，说明理由．
  ②求∠EGF的度数．（用含n的式子表示）
  
  组卷：311引用：3难度：0.2

  解析

• 25．如图，在平面直角坐标系中，已知A（2，0），以OA为一边在第四象限内画正方形OABC，D（m,0）为x轴上的一个动点（m＞2），以BD为一直角边在第四象限内画等腰直角△BDE，其中∠DBE=90°．
  （1）试判断线段AE、CD的数量关系，并说明理由；
  （2）设DE的中点为F，直线AF交y轴于点G．问：随着点D的运动，点G的位置是否会发生变化？若保持不变，请求出点G的坐标；若发生变化，请说明理由．
  组卷：2902引用：5难度：0.1

  解析