当前位置：试卷中心 > 试卷详情

2022-2023学年湖北省武汉市问津教育联合体高二（下）质检数学试卷（5月份）

发布：2024/7/9 8:0:8

一、单选题（本大题共8小题，共40分.在每小题列出的选项中，选出符合题目的一项）

1．在等比数列{a_n}中，有a₉a₁₁=a₇a₁₃，类比上述性质，在等差数列{b_n}中，有（　　）
A．b₉•b₁₁=b₇•b₁₃ B．b₈+b₉=b₁₀+b₁₁
C．b₈+b₁₀=b₉+b₁₁ D．b₆+b₁₄=b₉+b₁₁
组卷：12引用：4难度：0.7
解析
2．某数学兴趣小组把两个0、一个2、一个1与一个7组成一个五位数（如20107），若其中两个0不相邻，则这个五位数的个数为（　　）
A．18 B．36 C．72 D．144
组卷：39引用：3难度：0.7
解析
3．若函数
f
（
x
）
=
lnx
+
a
x
在[2，4]上为增函数，则a的取值范围为（　　）
A．（-∞，2] B．[2，+∞） C．（-∞，4] D．[4，+∞）
组卷：106引用：2难度：0.6
解析
4．现有天平及重量为1，2，4的砝码各一个，每一步，我们选取任意一个砝码，将其放入天平的左边或者右边，直至所有砝码全部放到天平两边，但在放的过程中发现天平的指针不会偏向分度盘的右边，则这样的放法共有（　　）种．
A．15 B．13 C．11 D．10
组卷：22引用：2难度：0.7
解析
5．已知数列满足a₁+2a₂+3a₃+…+na_n=n²，设b_n=na_n，则数列
{
1
b
n
b
n
+
1
}
的前2023项和为（　　）
A．
2022
4045
B．
4046
4047
C．
4044
4045
D．
2023
4047
组卷：500引用：7难度：0.6
解析
6．某人在19次射击中击中目标的次数为X，若X～B（19，0.8），若P（X=k）最大，则k=（　　）
A．14或15 B．15 C．15或16 D．16
组卷：279引用：1难度：0.6
解析
7．某卡车为乡村小学运送书籍，共装有10个纸箱，其中5箱英语书、5箱数学书．到目的地时发现丢失一箱，但不知丢失哪一箱．现从剩下9箱中任意打开两箱，结果都是英语书，则丢失的一箱也是英语书的概率为（　　）
A．
2
9
B．
3
8
C．
1
12
D．
5
8
组卷：44引用：2难度：0.7
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

四、解答题（本大题共6小题，共70分.解答应写出文字说明，证明过程或演算步骤）

21．杂交水稻的育种理论由袁隆平院士在1966年率先提出，1972年全国各地农业专家齐聚海南攻关杂交水稻育种，从此杂交水稻育种在袁隆平院士的理论基础上快速发展．截至2021年5月22日，中国国家水稻数据中心收录杂交水稻品种超1000种．如图为部分水稻稻种的生育期天数的频率分布直方图．

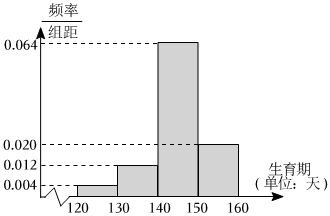
（1）根据频率分布直方图，估算水稻稻种生育期天数的平均值和第80百分位数；
（2）以频率视作概率，对中国国家水稻中心收录的所有稻种进行检验，
检验规定如下：①检验次数不超过5次；
②若检验出3个生育期超过中位数的稻种则检验结束．
设检验结束时，检验的次数为X，求随机变量X的分布列、期望和方差．
组卷：17引用：2难度：0.5
解析
22．设函数f（x）=-xlnx+ax²+x（a∈R）．
（1）若函数f（x）有两个不同的极值点，求实数a的取值范围；
（2）若a=1，k∈N，g（x）=x²+2x,当x＞2时，不等式2k（x-2）+f（x）＜g（x）恒成立，试求k的最大值．
组卷：65引用：4难度：0.2
解析

0/60 进入组卷

0/20 进入试卷篮

布置作业 发布测评 反向细目表 平行组卷 下载答题卡 试卷分析 在线训练 收藏试卷

充值会员，资源免费下载

A．b₉•b₁₁=b₇•b₁₃	B．b₈+b₉=b₁₀+b₁₁
C．b₈+b₁₀=b₉+b₁₁	D．b₆+b₁₄=b₉+b₁₁

2022-2023学年湖北省武汉市问津教育联合体高二（下）质检数学试卷（5月份）

一、单选题（本大题共8小题，共40分.在每小题列出的选项中，选出符合题目的一项）

1．在等比数列{an}中，有a9a11=a7a13，类比上述性质，在等差数列{bn}中，有（ ）

2．某数学兴趣小组把两个0、一个2、一个1与一个7组成一个五位数（如20107），若其中两个0不相邻，则这个五位数的个数为（ ）

3．若函数f（x）=lnx+ax在[2，4]上为增函数，则a的取值范围为（ ）

5．已知数列满足a1+2a2+3a3+…+nan=n2，设bn=nan，则数列{1bnbn+1}的前2023项和为（ ）

6．某人在19次射击中击中目标的次数为X，若X～B（19，0.8），若P（X=k）最大，则k=（ ）

7．某卡车为乡村小学运送书籍，共装有10个纸箱，其中5箱英语书、5箱数学书．到目的地时发现丢失一箱，但不知丢失哪一箱．现从剩下9箱中任意打开两箱，结果都是英语书，则丢失的一箱也是英语书的概率为（ ）

四、解答题（本大题共6小题，共70分.解答应写出文字说明，证明过程或演算步骤）

22．设函数f（x）=-xlnx+ax2+x（a∈R）．（1）若函数f（x）有两个不同的极值点，求实数a的取值范围；（2）若a=1，k∈N，g（x）=x2+2x,当x＞2时，不等式2k（x-2）+f（x）＜g（x）恒成立，试求k的最大值．

1．在等比数列{a_n}中，有a₉a₁₁=a₇a₁₃，类比上述性质，在等差数列{b_n}中，有（　　）

2．某数学兴趣小组把两个0、一个2、一个1与一个7组成一个五位数（如20107），若其中两个0不相邻，则这个五位数的个数为（　　）

3．若函数
f
（
x
）
=
lnx
+
a
x
在[2，4]上为增函数，则a的取值范围为（　　）

5．已知数列满足a₁+2a₂+3a₃+…+na_n=n²，设b_n=na_n，则数列
{
1
b
n
b
n
+
1
}
的前2023项和为（　　）

6．某人在19次射击中击中目标的次数为X，若X～B（19，0.8），若P（X=k）最大，则k=（　　）

7．某卡车为乡村小学运送书籍，共装有10个纸箱，其中5箱英语书、5箱数学书．到目的地时发现丢失一箱，但不知丢失哪一箱．现从剩下9箱中任意打开两箱，结果都是英语书，则丢失的一箱也是英语书的概率为（　　）

22．设函数f（x）=-xlnx+ax²+x（a∈R）．
（1）若函数f（x）有两个不同的极值点，求实数a的取值范围；
（2）若a=1，k∈N，g（x）=x²+2x,当x＞2时，不等式2k（x-2）+f（x）＜g（x）恒成立，试求k的最大值．