2022-2023学年贵州省遵义十一中八年级（上）第二次月考数学试卷

一、选择题（共48分）（每题4分）

• 1．以下列长度的三条线段为边，能组成三角形的是（　　）

  A．3，3，3

  B．3，3，6

  C．3，2，5

  D．3，2，6
  组卷：391引用：68难度：0.9

  解析

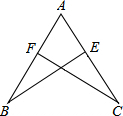• 2．如图，若△ABE≌△ACF，且AB=5，AE=2，则BF的长为（　　）

  A．2

  B．2.5

  C．3

  D．5
  组卷：30引用：2难度：0.6

  解析

• 3．下列运算正确的是（　　）

  A．m6÷m2=m3	B．（x+1）2=x2+1
  C．（3m2）3=9m6	D．2a3•a4=2a7
  组卷：1450引用：32难度：0.9

  解析

• 4．若一个多边形的内角和为1080°，则这个多边形的边数为（　　）

  A．6

  B．7

  C．8

  D．9
  组卷：3024引用：262难度：0.9

  解析

• 5．如图，已知AC=BD，添加下列一个条件后，仍无法判定△ABC≌△BAD的是（　　）

  A．∠ABC=∠BAD

  B．∠C=∠D=90°

  C．∠CAB=∠DBA

  D．CB=DA
  组卷：604引用：9难度：0.6

  解析

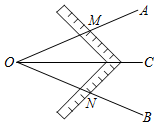• 6．工人师傅常用角尺平分一个任意角，具体做法如下：如图，已知∠AOB是一个任意角，在边OA，OB上分别取OM=ON，移动角尺，使角尺两边相同的刻度分别与点M，N重合，则过角尺顶点C的射线OC便是∠AOB角平分线．在证明△MOC≌△NOC时运用的判定定理是（　　）

  A．SSS

  B．SAS

  C．ASA

  D．AAS
  组卷：2079引用：21难度：0.6

  解析

• 7．将一副直角三角板按如图所示的方式叠放在一起，则图中∠α的度数是（　　）
  

  A．15°

  B．30°

  C．65°

  D．75°
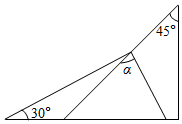  组卷：813引用：12难度：0.7

  解析

• 8．等腰三角形两边长分别为3，7，则它的周长为（　　）

  A．13

  B．17

  C．13或17

  D．不能确定
  组卷：493引用：40难度：0.9

  解析

三、解答题（共86分）

• 23．某学习小组学习了幂的有关知识发现：根据a^m=b,知道a、m可以求b的值．如果知道a、b,可以求m的值吗？他们为此进行了研究，规定：若a^m=b,那么T（a,b）=m.例如3⁴=81，那么T（3，81）=4．
  （1）填空：T（2，64）=

  ；
  （2）计算：T（3，27）+T（-2，-32）；
  （3）探索T（2，3）+T（2，7）与T（2，21）的大小关系，并说明理由．
  组卷：149引用：2难度：0.5

  解析

• 24．已知CD是经过∠BCA顶点C的一条直线，CA=CB．E、F分别是直线CD上两点，且∠BEC=∠CFA=∠α．
  （1）若直线CD经过∠BCA的内部，且E、F在射线CD上，请解决下面问题：
  ①如图1，若∠BCA=90°，∠α=90°，求证：BE=CF；
  ②如图2，若∠α+∠BCA=180°，探索三条线段EF、BE、AF的数量关系，并证明你的结论；
  （2）如图3，若直线CD经过∠BCA的外部，∠α=∠BCA，题（1）②中的结论是否仍然成立？若成立，请给予证明；若不成立，请你写出正确的结论再给予证明．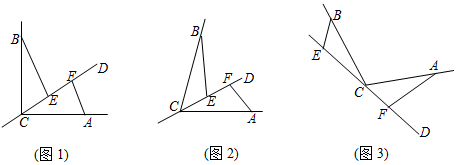
  
  组卷：345引用：4难度：0.6

  解析