2023-2024学年北京市东城区广渠门中学高二（上）月考数学试卷（10月份）

一、选择题共10小题，每小题5分，共50分.在每小题列出的四个选项中，选出符合题目要求的一项.

• 1．在空间直角坐标系中，点B是点A（1，2，3）在坐标平面xOy上的射影，O为坐标原点，则OB的长为（　　）

  A． 10

  B． 13

  C． 14

  D． 5
  组卷：63引用：2难度：0.9

  解析

• 2．设A，B是一个随机试验中的两个事件，则（　　）

  A．P（A∪B）=P（A）+P（B）	B．P（A）+P（B）≤1
  C．P（A∩B）=P（A）P（B）	D．若A⊆B，则P（A）≤P（B）
  组卷：945引用：9难度：0.7

  解析

• 3．抛掷3枚质地均匀的硬币，记事件A={至少1枚正面朝上}，事件B={至多2枚正面朝上}，事件C={没有硬币正面朝上}，则下列正确的是（　　）

  A．C=A∩B

  B．C=A∪B

  C．C⊆A

  D．C⊆B
  组卷：240引用：5难度：0.8

  解析

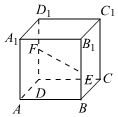• 4．如图，在平行六面体ABCD-A₁B₁C₁D₁中，E，F分别在棱BB₁和DD₁上，且BE=

  1

  3

  B

  B

  1

  ，DF=

  1

  2

  D

  D

  1

  ．若

  EF

  =

  x

  AB

  +

  y

  AD

  +

  z

  A

  A

  1

  ，则x+y+z=（　　）

  A．-1

  B．0

  C． 1 3

  D． 1 6
  组卷：94引用：3难度：0.8

  解析

• 5．在长方体ABCD-A₁B₁C₁D₁中，AB=BC=1，AA₁=

  3

  ，则异面直线AD₁与DB₁所成角的余弦值为（　　）

  A． 1 5

  B． 5 6

  C． 5 5

  D． 2 2
  组卷：7337引用：67难度：0.7

  解析

• 6．已知

  cos

  （

  α

  -

  π

  2

  ）

  =

  -

  3

  5

  ，

  α

  ∈

  （

  -

  π

  2

  ，

  0

  ）

  ，则sin2α的值为（　　）

  A． 1 25

  B． 24 25

  C．- 24 25

  D．- 1 25
  组卷：153引用：1难度：0.7

  解析

三、解答题共5小题，共75分。解答应写出文字说明，演算步骤或证明过程。

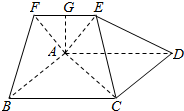• 19．如图，在五面体ABCDEF中，四边形 ABCD是边长为4的正方形，EF∥AD，平面ADEF⊥平面ABCD，且BC=2EF，AE=AF，点G是EF的中点．
  （1）证明：AG⊥平面ABCD．
  （2）若直线BF与平面ACE所成角的正弦值为

  6

  9

  ，求AG 的长．
  （3）判断线段AC上是否存在一点M，使MG∥平面ABF？若存在，求出

  AM

  MC

  的值；若不存在，说明理由．
  组卷：322引用：5难度：0.5

  解析

• 20．已知集合A_n={（x₁，x₂，⋯，x_n）|x_i∈{-1，1}（i=1，2，⋯，n）}．
  x,y∈A_n，x=（x₁，x₂，⋯，x_n），y=（y₁，y₂，⋯，y_n），其中x₁，y_i∈{-1，1}（i=1，2，⋯，n）．
  定义x⊙y=x₁y₁+x₂y₂+…+x_ny_n，若x⊙y=0，则称x与y正交．
  （Ⅰ）若x=（1，1，1，1），写出A₄中与x正交的所有元素；
  （Ⅱ）令B={x⊙y|x,y∈A_n}，若m∈B，证明：m+n为偶数；
  （Ⅲ）若A⊆A_n，且A中任意两个元素均正交，当n=14时，A中最多可以有多少个元素．
  组卷：36引用：2难度：0.2

  解析