2022-2023学年广东省佛山市顺德区卓越高中联考高一（上）期中数学试卷

一、单项选择题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.

• 1．已知集合A={x|y=

  1

  -

  x

  }，B={x|0＜x＜2}，则（∁_RA）∪B=（　　）

  A．（1，2）

  B．（0，1）

  C．（0，+∞）

  D．（-∞，2）
  组卷：114引用：3难度：0.9

  解析

• 2．命题“∀x＞2，x²+2＞6”的否定（　　）

  A．∃x≥2，x2+2＞6	B．∃x≤2，x2+2≤6
  C．∃x≤2，x2+2＞6	D．∃x＞2，x2+2≤6
  组卷：237引用：7难度：0.8

  解析

• 3．已知命题

  p

  ：

  1

  a

  ＞

  1

  4

  ，命题q：∀x∈R，ax²+ax+1＞0，则p成立是q成立的（　　）

  A．充分不必要条件	B．必要不充分条件
  C．充要条件	D．既不充分也不必要条件
  组卷：368引用：25难度：0.9

  解析

• 4．已知不等式ax²-bx-1≥0的解集是

  [

  -

  1

  2

  ，-

  1

  3

  ]

  ，则不等式x²-bx-a＜0的解集是（　　）

  A．（2，3）	B．（-∞，2）∪（3，+∞）
  C．（ 1 3 ， 1 2 ）	D．（-∞， 1 3 ）∪（ 1 2 ，+∞）
  组卷：2014引用：70难度：0.9

  解析

• 5．若函数f（x-1）=2x-5，且f（2a-1）=6，则a等于（　　）

  A． 4 3

  B． 7 3

  C． 11 4

  D． 7 4
  组卷：452引用：5难度：0.8

  解析

• 6．已知函数f（x）是定义在R上的偶函数，且在（0，+∞）上单调递减，f（-2）=0，则不等式xf（x）＞0的解集为（　　）

  A．（-∞，-2）∪（0，2）	B．（-∞，-2）∪（2，+∞）
  C．（-2，0）∪（0，2）	D．（-2，0）∪（2，+∞）
  组卷：487引用：11难度：0.8

  解析

• 7．已知集合A，B，定义A-B={x|x∈A且x∉B}，A+B={x|x∈A或x∈B}，则对于集合M，N下列结论一定正确的是（　　）

  A．M-（M-N）=N	B．（M-N）+（N-M）=∅
  C．（M+N）-M=N	D．（M-N）∩（N-M）=∅
  组卷：614引用：4难度：0.5

  解析

四、解答题：本题共6个大题，共70分，解答应写出文字说明、证明过程或演算步骤.

• 21．已知函数f（x）=-x²+（a+1）x（a∈R）．
  （1）若对于任意x∈[1，2]，恒有f（x）≥2x²成立，求实数a的取值范围；
  （2）若a≥2，求函数f（x）在区间[0，2]上的最大值g（a）．
  组卷：264引用：7难度：0.5

  解析

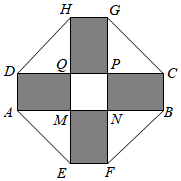• 22．如图，徐州某居民小区要建一座八边形的展馆区，它的主体造型的平面图是由两个相同的矩形ABCD和EFGH构成的面积为200m²的十字形地域，计划在正方形MNPQ上建一座花坛，造价为4200元/m²；在四个相同的矩形（图中阴影部分）上铺花岗岩地坪，造价为210元/m²；再在四个空角（图中四个三角形）铺草坪，造价为80元/m²．
  （1）设总造价为S（单位：元），AD长为x（单位：m），求出S关于x的函数关系式；
  （2）当AD长取何值时，总造价S最小，并求这个最小值．
  组卷：187引用：15难度：0.7

  解析