2022-2023学年浙江大学附中高一(下)期中数学模拟试卷
发布:2024/8/27 7:0:8
一.选择题(共8小题,满分40分,每小题5分)
-
1.已知集合
,B={x|x2-6x+8<0},则A∩B=( )A={x|x-1<2}组卷:51引用:5难度:0.8 -
2.设a,b∈R,则“
”是“a>1且b>1”的( )a+b>2ab>1组卷:64引用:3难度:0.7 -
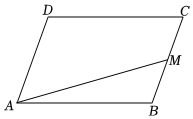 3.如图,在▱ABCD中,M为BC的中点,=mAC+nAM,则m+n=( )BD组卷:1435引用:3难度:0.9
3.如图,在▱ABCD中,M为BC的中点,=mAC+nAM,则m+n=( )BD组卷:1435引用:3难度:0.9 -
4.已知扇形的圆心角为120°,面积为
,则该扇形所在圆的半径为( )4π3组卷:389引用:4难度:0.8 -
5.已知角θ的终边经过点M(m,3-m),且tanθ=
,则m=( )12组卷:159引用:1难度:0.8 -
6.符合下列条件的三角形有且只有一个的是( )
组卷:145引用:3难度:0.8 -
7.将函数
的图象上所有点的横坐标伸长为原来的2倍,再将所得图象向右平移f(x)=sin(x2+π6)个单位长度,得到函数g(x)的图象,则下列说法正确的是( )π3组卷:193引用:3难度:0.5
四.解答题(共6小题,满分70分)
-
21.已知△ABC中,a,b,c分别为角A,B,C的对边,a(sinA-sinB)+bsinB=csinC.
(1)求角C的大小;
(2)若,且△ABC的面积为c=13,求△ABC的周长.33组卷:74引用:4难度:0.5 -
22.在△ABC中,内角A,B,C的对边分别为a,b,c,且
.acosC-12c=b
(1)求A;
(2)线段BC上一点D满足AD=BD=1,CD=3,求AB的长度.组卷:430引用:6难度:0.5


