2023-2024学年浙江省宁波市海曙区部分校八年级（上）期中数学试卷

一.选择题（共10小题，每小题3分，共计30分）

• 1．第19届杭州亚运会刚刚落下帷幕，在如图给出的运动图片中，属于轴对称图形的是（　　）

  A．

  B．

  C．

  D．
  组卷：22引用：1难度：0.8

  解析

• 2．下列各组长度的三条线段能组成三角形的是（　　）

  A．1，2，3

  B．1，1，2

  C．1，2，2

  D．1，5，7
  组卷：1809引用：21难度：0.9

  解析

• 3．下列选项中，可以用来证明命题“若|a-1|＞1，则a＞2”是假命题的反例是（　　）

  A．a=2

  B．a=1

  C．a=0

  D．a=-1
  组卷：786引用：13难度：0.9

  解析

• 4．下列用数轴表示不等式组

  x ＞ 1

  x ≤ 2

  的解集正确的是（　　）

  A．	B．
  C．	D．
  组卷：3994引用：34难度：0.9

  解析

• 5．用三角板作△ABC的边BC上的高，下列三角板的摆放位置正确的是（　　）

  A．	B．
  C．	D．
  组卷：7177引用：100难度：0.9

  解析

• 6．如图，直线a∥b,点A和点B分别在直线a和b上，点C在直线a、b之间，且BC=AC，∠ACB=120°，∠1=45°，则∠2的度数是（　　）

  A．60°

  B．65°

  C．70°

  D．75°
  组卷：290引用：2难度：0.9

  解析

• 7．若关于x的不等式（1-a）x＞3的解集为

  x

  ＜

  3

  1

  -

  a

  ，则a的取值范围是（　　）

  A．a＜1

  B．a＞1

  C．a≠1

  D．a＜-1
  组卷：450引用：1难度：0.9

  解析

三.解答题（共7小题，满分66分）

• 22．【概念认识】
  如图①，在△ABC中，若∠ABD=∠DBE=∠EBC，则BD，BE叫做∠ABC的“三分线”．其中，BD是“邻AB三分线”，BE是“邻BC三分线”．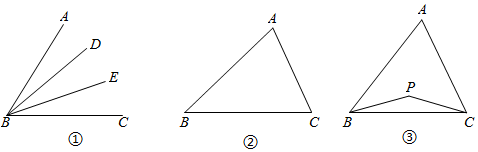
  
  【问题解决】
  （1）如图②，在△ABC中，∠A=80°，∠B=45°，若∠B的三分线BD交AC于点D，求∠BDC的度数；
  （2）如图③，在△ABC中，BP、CP分别是∠ABC邻BC三分线和∠ACB邻BC三分线，且∠BPC=140°，求∠A的度数；
  【延伸推广】
  （3）在△ABC中，∠ACD是△ABC的外角，∠B的三分线所在的直线与∠ACD的三分线所在的直线交于点P．若∠A=m°（m＞54），∠B=54°，直接写出∠BPC的度数．（用含m的代数式表示）
  组卷：2877引用：18难度：0.1

  解析

• 23．阅读材料：
  （1）对于任意两个数a、b的大小比较，有下面的方法：
  当a-b＞0时，一定有a＞b；
  当a-b=0时，一定有a=b；
  当a-b＜0时，一定有a＜b.
  反过来也成立．因此，我们把这种比较两个数大小的方法叫做“求差法”．
  （2）对于比较两个正数a、b的大小时，我们还可以用它们的平方进行比较：
  ∵a²-b²=（a+b）（a-b），a+b＞0
  ∴（a²-b²）与（a-b）的符号相同
  当a²-b²＞0时，a-b＞0，得a＞b
  当a²-b²=0时，a-b=0，得a=b
  当a²-b²＜0时，a-b＜0，得a＜b
  解决下列实际问题：
  （1）课堂上，老师让同学们制作几种几何体，张丽同学用了3张A4纸，7张B5纸；李明同学用了2张A4纸，8张B5纸．设每张A4纸的面积为x,每张B5纸的面积为y,且x＞y,张丽同学的用纸总面积为W₁，李明同学的用纸总面积为W₂．回答下列问题：
  ①W₁=

  （用x、y的式子表示）
  W₂=

  （用x、y的式子表示）
  ②请你分析谁用的纸面积最大．
  （2）如图1所示，要在燃气管道l上修建一个泵站，分别向A、B两镇供气，已知A、B到l的距离分别是3km、4km（即AC=3km,BE=4km），AB=x km,现设计两种方案：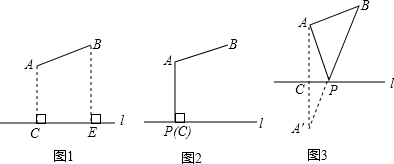
  
  方案一：如图2所示，AP⊥l于点P，泵站修建在点P处，该方案中管道长度a₁=AB+AP．
  方案二：如图3所示，点A′与点A关于l对称，A′B与l相交于点P，泵站修建在点P处，该方案中管道长度a₂=AP+BP．
  ①在方案一中，a₁=

  km（用含x的式子表示）；
  ②在方案二中，a₂=

  km（用含x的式子表示）；
  ③请你分析要使铺设的输气管道较短，应选择方案一还是方案二．
  组卷：1476引用：4难度：0.5

  解析