2023-2024学年贵州省铜仁一中高二（上）质检数学试卷（一）（8月份）

一、单项选择题：本大题共8个小题，每小题5分，共40分。

• 1．设集合A={x|x²-5x-6≤0}，函数y=ln（4-x）的定义域为B，则A∩B=（　　）

  A．[2，4）

  B．[-1，4）

  C．[-1，4]

  D．[-6，4）
  组卷：16引用：2难度：0.8

  解析

• 2．已知向量

  a

  =

  （

  sinα

  ，-

  3

  ）

  ，

  b

  =

  （

  1

  ，

  cosα

  ）

  ，若

  a

  ⊥

  b

  ，则

  tan

  （

  α

  +

  π

  4

  ）

  =（　　）

  A． - 1 2

  B． 1 2

  C．-2

  D．2
  组卷：37引用：3难度：0.8

  解析

• 3．设a=3^0.1，b=lg5-lg2，

  c

  =

  log

  3

  9

  10

  ，则a,b,c的大小关系是（　　）

  A．b＞c＞a

  B．a＞c＞b

  C．b＞a＞c

  D．a＞b＞c
  组卷：44引用：5难度：0.9

  解析

• 4．下列结论中正确是（　　）

  A．若直线a,b为异面直线，则过直线a与直线b平行的平面有无数多个

  B．若平面α∥平面β，直线m⊂α，点M∈β，则过点M有且只有一条直线与m平行

  C．若直线m与平面α内无数条直线平行，则直线m与平面α平行

  D．若直线l⊥平面α，则过直线l与平面α垂直的平面有且只有一个
  组卷：143引用：5难度：0.7

  解析

• 5．甲、乙、丙三人相互做传球训练，第1次由甲将球传出，每次传球时，传球者都等可能地将球传给另外两个人中的任何一人，则6次传球后球在甲手中的概率为（　　）

  A． 11 32

  B． 31 96

  C． 5 16

  D． 17 48
  组卷：311引用：5难度：0.5

  解析

• 6．在三棱锥P-ABC中，PA⊥平面ABC，

  ∠

  BAC

  =

  π

  2

  ，AB=AC=AP=2，则三棱锥外接球的表面积为（　　）

  A．4π

  B．12π

  C． 40 3 π

  D．16π
  组卷：109引用：3难度：0.5

  解析

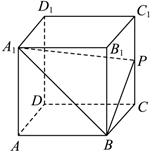• 7．如图，在棱长为4的正方体ABCD-A₁A₁C₁D₁中，点P是CC₁的中点，动点Q在平面DCC₁D₁内（包括边界），若AQ∥平面A₁BP，则AQ的最小值是（　　）

  A．2

  B． 2 2

  C． 2 5

  D． 3 2
  组卷：45引用：3难度：0.5

  解析

四、解答题：本题共6个小题，共70分。应写出相关演算步骤的计算公式或文字说明。

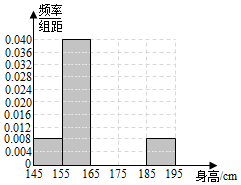• 21．某校有高中生2000人，其中男女生比例约为5：4，为了获得该校全体高中生的身高信息，采取了以下两种方案：
  方案一：采用比例分配的分层随机抽样方法，抽收了样本容量为n的样本，得到频数分布表和频率分布直方图．
  方案二：采用分层随机抽样方法，抽取了男、女生样本容量均为25的样本，计算得到男生样本的均值为170，方差为16，女生样本的均值为160，方差为20．
  

  身高（单位：cm）	[145，155）	[155，165）	[165，175）	[175，185）	[185，195]
  频数	m	p	q	6	4

  （1）根据图表信息，求n,q并补充完整频率分布直方图，估计该校高中生的身高均值；（同一组中的数据以这组数据所在区间中点的值为代表）
  （2）计算方案二中总样本的均值及方差；
  （3）计算两种方案总样本均值的差，并说明用方案二总样本的均值作为总体均值的估计合适吗？为什么？
  组卷：266引用：4难度：0.4

  解析

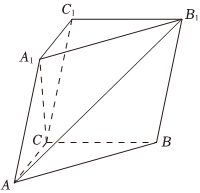• 22．在三棱柱ABC-A₁B₁C₁中，A₁C⊥底面ABC，∠ACB=90°，AA₁=2，A₁到平面BCC₁B₁的距离为1．
  （1）证明：A₁C=AC；
  （2）已知AA₁与BB₁的距离为2，求AB₁与平面BCC₁B₁所成角的正弦值．
  组卷：304引用：3难度：0.5

  解析