2022-2023学年广西南宁二中高二(下)期末数学试卷
发布:2024/6/8 8:0:9
一、选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
-
1.设U=R,已知集合A={x|x≥1},B={x|x>a},且(∁UA)∪B=R,则实数a的取值范围是( )
组卷:821引用:13难度:0.9 -
2.复数
=( )2i2-i组卷:18引用:8难度:0.9 -
3.若向量
,a的夹角为b,且|π3|=2,|a|=1,则向量|b+2a|为( )b组卷:447引用:3难度:0.8 -
4.已知圆锥的侧面展开图是一个半径为4,弧长为4π的扇形,则该圆锥的表面积为( )
组卷:552引用:3难度:0.9 -
5.设O为正方形ABCD的中心,在O,A,B,C,D中任取3点,则取到的3点共线的概率为( )
组卷:3512引用:16难度:0.8 -
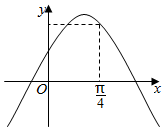 6.已知函数f(x)=sin(2x+φ)的部分图象如图所示,且经过点,则( )A(π4,32)组卷:191引用:4难度:0.6
6.已知函数f(x)=sin(2x+φ)的部分图象如图所示,且经过点,则( )A(π4,32)组卷:191引用:4难度:0.6 -
7.已知a,b∈(0,3),且4lna=aln4,4lnb=bln2,c=log0.30.06,则( )
组卷:224引用:4难度:0.6
四、解答题:本大题共6小题,共70分、解答应写出文字说明、证明过程或演算步骤.
-
21.已知双曲线
的一条渐近线方程为C:x2a2-y2b2=1(a>0,b>0),且双曲线经过点A(2,2).2x-y=0
(1)求双曲线C的方程;
(2)过点B(1,0)且斜率不为0的直线与C交于M,N两点(与点A不重合),直线AM,AN分别与直线x=1交于点P,Q,求的值.|PB||QB|组卷:222引用:6难度:0.2 -
22.已知函数f(x)=2ax-axcosx,g(x)=sinx.
(1)当x∈[0,π]时,若a=1,证明:f(x)≥g(x);
(2)当x>0时,f(x)≥g(x),求a的取值范围.组卷:24引用:2难度:0.5


