2022-2023学年河北省保定市六校联盟高二（下）联考数学试卷（4月份）

一、选择题：本题共8小题，每小题3分，共040分，在每小题给出的四个选项中，只有一项是符合题目要求的.

• 1．已知集合A={x|x²＜9}，B={x|-1＜x＜5，x∈N}，则A∩B=（　　）

  A．（-1，3）

  B．（0，5）

  C．{1，2}

  D．{0，1，2}
  组卷：94引用：6难度：0.8

  解析

• 2．函数

  f

  （

  x

  ）

  =

  lo

  g

  2

  1

  x

  的导函数为（　　）

  A． f ′ （ x ） = ln 2 x	B． f ′ （ x ） = 1 xln 2
  C． f ′ （ x ） = - ln 2 x	D． f ′ （ x ） = - 1 xln 2
  组卷：320引用：8难度：0.7

  解析

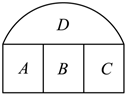• 3．如图，提供4种不同的颜色给图中A，B，C，D四块区域涂色，若相邻的区域不能涂同一种颜色，则不同的涂法共有（　　）种

  A．12

  B．36

  C．48

  D．72
  组卷：230引用：4难度：0.5

  解析

• 4．设函数

  f

  （

  x

  ）

  =

  1

  3

  x

  -

  lnx

  （

  x

  ＞

  0

  ）

  ，则y=f（x）（　　）

  A．在区间 （ 1 e ， 1 ） 递减	B．在区间（0，3）上递增
  C．在点x=3处有极大值	D．在区间（3，+∞）上递减
  组卷：116引用：1难度：0.8

  解析

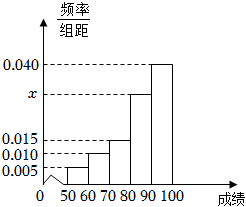• 5．某中学全体学生参加了数学竞赛，随机抽取了400名学生进行成绩统计，发现抽取的学生的成绩都在50分至100分之间，进行适当分组后（每组为左闭右开的区间），画出频率分布直方图如图所示，下列说法正确的是（　　）

  A．直方图中x的值为0.035

  B．在被抽取的学生中，成绩在区间[70，80）的学生数为30人

  C．估计全校学生的平均成绩为83分

  D．估计全校学生成绩的样本数据的80%分位数约为95分
  组卷：363引用：7难度：0.8

  解析

• 6．某企业的一批产品由一等品零件、二等品零件混装而成，每包产品均含有10个零件．小张到该企业采购，利用如下方法进行抽检：从该企业产品随机抽取1包产品，再从该包产品中随机抽取4个零件，若抽取的零件都是一等品，则决定采购该企业产品；否则，拒绝采购．假设该企业这批产品中，每包产品含1个或2个二等品零件，其中含2个二等品零件的包数占10%，则小张决定采购该企业产品的概率为（　　）

  A． 1 30

  B． 43 75

  C． 3 50

  D． 1 10
  组卷：15引用：1难度：0.8

  解析

• 7．已知函数f（x）及其导函数f'（x）的定义域均为R，f（2x+3）是偶函数，记g（x）=f'（x），g（x+2）也是偶函数，则f'（2023）的值为（　　）

  A．-2

  B．0

  C．-1

  D．2
  组卷：64引用：1难度：0.5

  解析

四、解答题：本题共6小题，共70分.解答应写出文字说明，证明过程或演算步骤.

• 21．法国数学家庞加莱是个喜欢吃面包的人，他每天都会到同一家面包店购买一个面包．该面包店的面包师声称自己所出售的面包的平均质量是1000 g,上下浮动不超过50 g.这句话用数学语言来表达就是：每个面包的质量服从期望为1000 g,标准差为50 g的正态分布．
  （1）已知如下结论：若X～N（μ，σ²），从X的取值中随机抽取k（k∈N^*，k≥2）个数据，记这k个数据的平均值为Y，则随机变量

  Y

  ～

  N

  （

  μ

  ，

  σ

  2

  k

  ）

  ．利用该结论解决下面问题．
  （ⅰ）假设面包师的说法是真实的，随机购买25个面包，记随机购买25个面包的平均值为Y，求P（Y≤980）；
  （ⅱ）庞加莱每天都会将买来的面包称重并记录，25天后，得到的数据都落在（950，1050）上，并经计算25个面包质量的平均值为978.72 g.庞加莱通过分析举报了该面包师，从概率角度说明庞加莱举报该面包师的理由；
  （2）假设有两箱面包（面包除颜色外，其他都一样），已知第一箱中共装有6个面包，其中黑色面包有2个；第二箱中共装有8个面包，其中黑色面包有3个．现随机挑选一箱，然后从该箱中随机取出2个面包．求取出黑色面包个数的分布列及数学期望．
  附：
  ①随机变量η服从正态分布N（μ，σ²），则P（μ-σ≤η≤μ+σ）=0.6827，P（μ-2σ≤η≤μ+2σ）=0.9545，P（μ-3σ≤η≤μ+3σ）=0.9973；
  ②通常把发生概率小于0.05的事件称为小概率事件，小概率事件基本不会发生．
  组卷：276引用：9难度：0.5

  解析

• 22．设函数f（x）=x²-ax-a²lnx.（a∈R）
  （1）当a=2时，讨论函数y=f（x）的单调性；
  （2）曲线y=f（x）与直线y=m交于A（x₁，y₁），B（x₂，y₂）两点，求证：

  f

  ′

  （

  x

  1

  +

  x

  2

  2

  ）

  ＞

  0

  ．
  组卷：18引用：1难度：0.5

  解析