当前位置：试卷中心 > 试卷详情

2023-2024学年江苏省苏州外国语学校九年级（上）月考数学试卷（10月份）

发布：2024/9/8 5:0:8

一、单选题（本大题共8小题，每题3分，共24分）

1．下列方程是一元二次方程的是（　　）
A．ax²+bx+c=0 B．x²-y+1=0 C．x²=0 D．
1
x
2
+x=2
组卷：397引用：18难度：0.9
解析
2．已知三角形的两边长为3和6，第三边的长是方程x²-7x+12=0的一个根，则这个三角形的周长是（　　）
A．12 B．13 C．12或13 D．15
组卷：142引用：1难度：0.5
解析
3．下列对二次函数y=-（x+1）²-3的图象描述不正确的是（　　）
A．开口向下
B．顶点坐标为（-1，-3）
C．与y轴相交于点（0，-3）
D．当x＞1时，函数值y随x的增大而减小
组卷：201引用：4难度：0.6
解析
4．在同一平面直角坐标系中，函数y=ax²+b与y=ax+b（a,b都不为0）的图象的相对位置可以是（　　）
A． B． C． D．
组卷：3483引用：9难度：0.5
解析
5．如图①，“东方之门”通过简单的几何曲线处理，将传统文化与现代建筑融为一体，最大程度地传承了苏州的历史文化．如图②，“门”的内侧曲线呈抛物线形，已知其底部宽度为80米，高度为200米．则离地面150米处的水平宽度（即CD的长）为（　　）
A．40米 B．30米 C．25米 D．20米
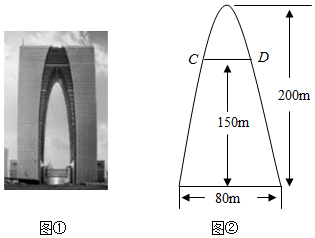组卷：690引用：4难度：0.6
解析
6．定义[a,b,c]为函数y=ax²+bx+c的特征数，下面给出特征数为[m-1，1+m,-2m]的函数的一些结论：①当m=3时，函数图象的顶点坐标是（-1，-8）；②当m＞1时，函数图象截x轴所得的线段长度大于3；③当m＜0时，函数在x＞
1
2
时，y随x的增大而减小；④不论m取何值，函数图象经过两个定点．其中正确的结论有（　　）
A．1个 B．2个 C．3个 D．4个
组卷：313引用：3难度：0.7
解析
7．平面直角坐标系xOy中，P点坐标为（m,2n²-10），且实数m,n满足2m-3n²+9=0则点P到原点O的距离的最小值为（　　）
A．
3
5
10
B．
12
5
C．
6
5
3
D．
4
5
5
组卷：618引用：3难度：0.4
解析
8．定义：我们将顶点的横坐标和纵坐标互为相反数的二次函数称为“互异二次函数”．如图，在正方形OABC中，点A（0，2），点C（2，0），则互异二次函数y=（x-m）²-m与正方形OABC有交点时m的最大值和最小值分别是（　　）
A．4，-1 B．
5
-
17
2
，-1 C．4，0 D．
5
+
17
2
，-1
组卷：3212引用：28难度：0.4
解析

二、填空题（本大题共8小题，每题3分，共24分）

9．已知一元二次方程x²-14x+48=0的两个根是菱形的两条对角线长，则这个菱形的周长
．
组卷：883引用：15难度：0.6
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

三、解答题（本大题共11小题，共82分）

26．端午节前夕，某超市从厂家分两次购进A、B两种品牌的粽子，两次进货时，两种品牌粽子的进价不变．第一次购进A品牌粽子100袋和B品牌粽子150袋，总费用为7000元；第二次购进A品牌粽子180袋和B品牌粽子120袋，总费用为8100元．
（1）求A、B两种品牌粽子每袋的进价各是多少元；
（2）当B品牌粽子销售价为每袋54元时，每天可售出20袋，为了促销，该超市决定对B品牌粽子进行降价销售．经市场调研，若每袋的销售价每降低1元，则每天的销售量将增加5袋．当B品牌粽子每袋的销售价降低多少元时，每天售出B品牌粽子所获得的利润最大？最大利润是多少元？
组卷：3610引用：12难度：0.5
解析
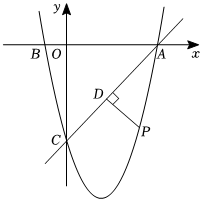27．如图，在直角坐标系中，已知点B的坐标为（-2，0），且OA=OC=8，抛物线y=ax²+bx+c（a≠0）的图象经过A，B，C三点．
（1）求抛物线的表达式；
（2）若点P是直线AC下方的抛物线上的一个动点，作PD⊥AC于点D，当PD的值最大时，求此时点P的坐标；
（3）在（2）的条件下，E为AC直线上一动点，F为对称轴上一动点，当A，P，E，F四个点为顶点的四边形为平行四边形时，求E点的坐标．
组卷：447引用：2难度：0.4
解析