当前位置：试卷中心 > 试卷详情

2022-2023学年北京市海淀区师达中学九年级（上）段考数学试卷（11月份）

发布：2024/8/22 1:0:1

一、选择题（共16分，每题2分）第1-8题均有四个选项，符合题意的选项只有一个．

1．古典园林中的窗户是中国传统建筑装饰的重要组成部分，一窗一姿容，一窗一景致．下列窗户图案中，是中心对称图形的是（　　）
A． B． C． D．
组卷：285引用：22难度：0.9
解析
2．二次函数y=2（x-3）²+1的图象的顶点坐标是（　　）
A．（2，3） B．（2，1） C．（3，-1） D．（3，1）
组卷：962引用：16难度：0.8
解析
3．用配方法解方程x²+4x=1，变形后结果正确的是（　　）
A．（x-2）²=2 B．（x+2）²=2 C．（x-2）²=5 D．（x+2）²=5
组卷：155引用：19难度：0.6
解析
4．不透明的袋子中装有2个红球，3个黑球，这些球除颜色外无其他差别．从袋子中随机摸出一个球，则摸出红球的概率是（　　）
A．
2
5
B．
3
5
C．
2
3
D．
1
2
组卷：177引用：7难度：0.6
解析
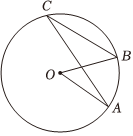5．如图，OA，OB是⊙O的半径，若∠AOB=50°，则∠ACB的度数是（　　）
A．25° B．50° C．75° D．100°
组卷：395引用：6难度：0.9
解析
6．根据圆规作图的痕迹，可用直尺成功地找到三角形内心的是（　　）
A． B． C． D．
组卷：1020引用：30难度：0.8
解析
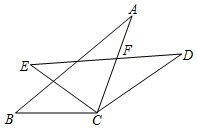7．如图，在△ABC中，以C为中心，将△ABC顺时针旋转35°得到△DEC，边ED，AC相交于点F，若∠A=30°，则∠EFC的度数为（　　）
A．60° B．65° C．72.5° D．115°
组卷：1655引用：25难度：0.5
解析
8．在平面直角坐标系xOy中，点（-1，y₁），（2，y₂），（4，y₃）在抛物线y=ax²-2ax+c上，当a＞0时，下列说法一定正确的是（　　）
A．若y₁y₂＜0，则y₃＞0 B．若y₂y₃＞0，则y₁＜0
C．若y₁y₃＜0，则y₂＞0 D．若y₁y₂y₃=0，则y₂=0
组卷：1661引用：15难度：0.5
解析

二、填空题（本题共16分，每小题2分）

9．在平面直角坐标系xOy中，点（4，-7）关于原点的对称点坐标为
．
组卷：142引用：7难度：0.9
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

三、解答题（共68分，第17-22题，每题5分，第23-26题，每题6分，第27-28题，每题7分）

27．点M为正方形ABCD的边BC延长线上一点，

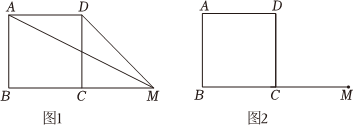
（1）如图1，当BC=CM=3时，连接AM，DM，则∠BMD=
°，AM=
；
（2）如图2，将射线BM绕点B逆时针旋转α（0°＜α＜40°）得到射线BF，作AH⊥BF于点H，在射线BF上取点E，使得BE=2AH，连接DE．
①依题意补全图形；
②猜想∠BED的度数，并证明．
组卷：34引用：2难度：0.5
解析
28．在平面直角坐标系xOy中，已知⊙O的半径为2，对于点P，直线l和⊙O，给出如下定义：若点P关于直线l对称的点在⊙O上或⊙O的内部，则称点P为⊙O关于l的反射点．

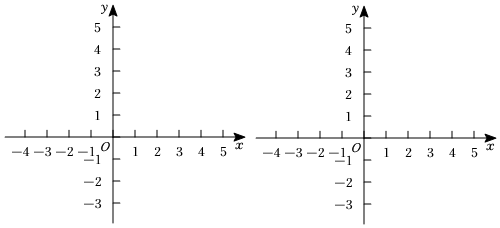
（1）已知直线l为直线x=3，
①在点P₁（4，0），P₂（4，1），P₃（5，1）中，是⊙O关于l的反射点的有
；
②若点P为x轴上的动点，且点P为⊙O关于l的反射点，则点P的横坐标的最大值为
；
（2）已知直线l的解析式为y=kx+2（k≠0），
①当k=-1时，若点P为直线x=
18
5
上的动点，且点P为⊙O关于l的反射点，则点P的纵坐标t的取值范围是
；
②点
B
（
3
，
3
）
，
C
（
3
，
1
）
，若线段BC的任意一点都为⊙O关于l的反射点，则k的取值范围是
．
组卷：15引用：2难度：0.5
解析