在平面直角坐标系xOy中，已知⊙O的半径为2，对于点P，直线l和⊙O，给出如下定义：若点P关于直线l对称的点在⊙O上或⊙O的内部，则称点P为⊙O关于l的反射点．
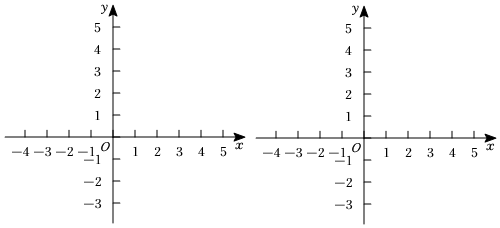
（1）已知直线l为直线x=3，
①在点P1（4，0），P2（4，1），P3（5，1）中，是⊙O关于l的反射点的有 P1，P3P1，P3；
②若点P为x轴上的动点，且点P为⊙O关于l的反射点，则点P的横坐标的最大值为 88；
（2）已知直线l的解析式为y=kx+2（k≠0），
①当k=-1时，若点P为直线x=185上的动点，且点P为⊙O关于l的反射点，则点P的纵坐标t的取值范围是 45≤t≤16545≤t≤165；
②点B（3，3），C（3，1），若线段BC的任意一点都为⊙O关于l的反射点，则k的取值范围是 -3＜k＜-33-3＜k＜-33．
18
5
4
5
≤
t
≤
16
5
4
5
≤
t
≤
16
5
B
（
3
，
3
）
C
（
3
，
1
）
-
3
＜
k
＜
-
3
3
-
3
＜
k
＜
-
3
3
【考点】圆的综合题．
【答案】P1，P3；8；；
4
5
≤
t
≤
16
5
-
3
＜
k
＜
-
3
3
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/8/22 1:0:1组卷：16引用：2难度：0.5
相似题
-
1．如图1，已知点A（6，0），B（0，6），点C在半径为3的⊙O上运动，将OC顺时针旋转90°得到OD．
（1）当OC∥AB时，则∠BOC=°；
（2）如图2，若点E在线段AB上运动，连接DE，AC，BC．
①线段DE长度的最小值是 ；
②△ABC的面积最大值是 ．
（3）如图3，连接AD，BC．
①当OC∥AD时，求证：BC是⊙O的切线；
②在整个运动过程中，若直线AD，BC交于点P，则下列命题错误的是 ．
A．线段AD，BC的关系为互相垂直且相等
B．点P的纵坐标的最小值为3-32
C．点P的纵坐标的最大值为3+32
D．点P的运动轨迹为圆弧，该圆弧长为2π2
发布：2025/6/17 6:30:2组卷：90引用：1难度：0.1 -
2．已知，在Rt△ABC中，∠A=90°，AB=3，AC=4，⊙A与⊙B外切于点D，并分别与BC、AC边交于点E、F．
（1）设EC=x,FC=y,求y关于x的函数关系式，并写出自变量x的取值范围；
（2）若以E、F、C为顶点的三角形与△ABC相似，求的值；ADBD
（3）若⊙C与⊙A、⊙B都相切，求的值．ADBD发布：2025/6/17 21:0:1组卷：22引用：1难度：0.3 -
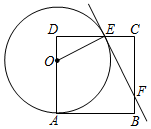3．如图，在边长为8的正方形ABCD中，点O为AD上一动点（4＜OA＜8），以O为圆心，OA的长为半径的⊙O交边CD于点E，连接OE，过点E作⊙O的切线交边BC于点F．
（1）求证：△ODE∽△ECF；
（2）设DE=x,求OA的长（用含x的代数式表示）；
（3）在点O运动的过程中，设△CEF的周长为p,试用含x的代数式表示p,你能发现怎样的结论？发布：2025/6/17 21:30:1组卷：37引用：1难度：0.4
