2023-2024学年北京二中航班九年级(上)月考数学试卷(10月份)
发布:2024/9/21 4:0:8
一、选择题。(共10小题,每小题3分,共30分)
-
1.已知集合A={x∈R|3x+2>0},B={x∈R|(x+1)(x-3)>0},则A∩B=( )
组卷:39引用:1难度:0.7 -
2.将抛物线y=6x2先向左平移2个单位,再向上平移3个单位后得到新的抛物线,则新抛物线解析式是( )
组卷:50引用:3难度:0.7 -
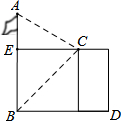 3.如图,某人站在楼顶观测对面的笔直的旗杆AB,已知观测点C到旗杆的距离CE=8m,测得旗杆的顶部A的仰角∠ECA=30°,旗杆底部B的俯角∠ECB=45°,那么旗杆AB的高度是( )组卷:209引用:5难度:0.7
3.如图,某人站在楼顶观测对面的笔直的旗杆AB,已知观测点C到旗杆的距离CE=8m,测得旗杆的顶部A的仰角∠ECA=30°,旗杆底部B的俯角∠ECB=45°,那么旗杆AB的高度是( )组卷:209引用:5难度:0.7 -
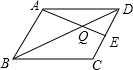 4.如图,在平行四边形ABCD中,E为DC边的中点,AE交BD于点Q,若△DQE的面积为9,则△AQB的面积为( )组卷:230引用:4难度:0.9
4.如图,在平行四边形ABCD中,E为DC边的中点,AE交BD于点Q,若△DQE的面积为9,则△AQB的面积为( )组卷:230引用:4难度:0.9 -
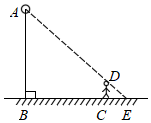 5.如图,身高1.6米的小慧同学从一盏路灯下的B处向前走了8米到达点C处时,发现自己在地面上的影子CE的长是2米,则路灯AB的高为( )组卷:223引用:4难度:0.5
5.如图,身高1.6米的小慧同学从一盏路灯下的B处向前走了8米到达点C处时,发现自己在地面上的影子CE的长是2米,则路灯AB的高为( )组卷:223引用:4难度:0.5 -
6.已知集合A={x|x<a},B={x|1≤x≤2},且A∪B=A,则实数a的取值范围是( )
组卷:57引用:1难度:0.7 -
7.函数y=f(x)的定义域是R,该函数关于y轴对称,且在(-∞,0]上是增函数,若f(a)≤f(2),则实数a的取值范围是( )
组卷:4引用:1难度:0.5 -
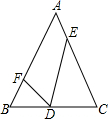 8.已知D、E、F分别为等腰△ABC边BC、CA、AB上的点,如果AB=AC,BD=2,CD=3,CE=4,AE=,∠FDE=∠B,那么AF的长为( )32组卷:355引用:3难度:0.9
8.已知D、E、F分别为等腰△ABC边BC、CA、AB上的点,如果AB=AC,BD=2,CD=3,CE=4,AE=,∠FDE=∠B,那么AF的长为( )32组卷:355引用:3难度:0.9
三、解答题。(第19~20题每小题4分,第21~23题每小题4分,第24题6分,共38分)
-
23.问题背景:
(1)如图1,已知△ABC∽△ADE,求证:△ABD∽△ACE;
尝试应用:
(2)如图2,在△ABC和△ADE中,∠BAC=∠DAE=90°,∠ABC=∠ADE=30°,AC与DE相交于点F,点D在BC边上,BD=3,CD=5,求的值;DFCF
灵活运用:
(3)如图3,点A是△BCD内一点,∠ADB=∠ABC=30°,∠BAC=90°,BD=3,CD=,直接写出AD的长.7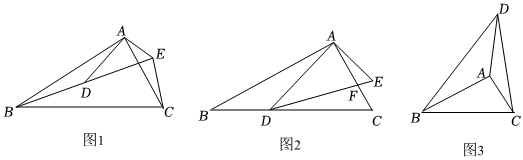 组卷:134引用:3难度:0.3
组卷:134引用:3难度:0.3 -
24.在平面直角坐标系中,O为坐标原点,对任意的点P(x,y),定义∥OP∥=|x|+|y|,任取点A(x1,y1),B(x2,y2),记A'(x1,y2),B'(x2,y1),若此时满足:||OA||2+||OB||2≥||OA'||2+||OB'||2成立,则称点A与点B相关.
(1)分别判断下面各组中两点是否相关,并说明理由:
①A(-2,1),B(3,2);
②C(4,-3),D(2,4).
(2)给定n∈N*,n≥3,点集:Ωn={(x,y)|-n≤x≤n,-n≤y≤n,x,y∈Z},求集合Ωn中与点A(1,1)相关的点的个数.组卷:8引用:1难度:0.3


