当前位置：试卷中心 > 试卷详情

2023年黑龙江省佳木斯一中高考数学第一次调研试卷

发布：2024/6/17 8:0:9

一．单选题（本题共8道小题，每题5分，共40分）

1．
A
=
{
x
|
|
x
|
≥
1
}
，
B
=
{
x
|
x
-
5
x
-
1
≤
0
，
x
∈
N
}
，则A∩B=（　　）
A．[1，5] B．（1，5]
C．{0，1，2，3，4，5} D．{2，3，4，5}
组卷：227引用：3难度：0.8
解析
2．设命题p：∃x₀＜0，使得x₀+1＞0，则￢p为（　　）
A．∃x₀＜0，使得x₀+1≤0 B．∃x₀≥0，使得x₀+1＞0
C．∀x＜0，都有x+1≤0 D．∀x≥0，都有x+1＞0
组卷：149引用：4难度：0.7
解析
3．下列命题为真命题的是（　　）
A．若a＞b＞0，则ac²＞bc² B．若a＜b＜0，则
1
a
＜
1
b
C．若a＜b＜0，则a²＜ab＜b² D．若a＞b＞0，则a²＞b²
组卷：966引用：19难度：0.9
解析
4．十九世纪下半叶集合论的创立．奠定了现代数学的基础．著名的“康托三分集．（Cantor）”是数学理性思维的构造产物，具体典型的分形特征，其操作过程如下：将闭区间[0，1]均分为三段，去掉中间的开区间段（
1
3
，
2
3
），记为第一次操作；再将剩下的两个区间
[
0
，
1
3
]
，
[
2
3
，
1
]
分别均分为三段，并各自去掉中间的开区间段，记为第二次操作；……如此这样，每次在上一次操作的基础上，将剩下的各个区间分别均分为三段，同样各自去掉中间的开区间段．操作过程不断地进行下去．以至无穷，剩下的区间集合即“康托三分集”．第三次操作后，从左到右第四个区间为（　　）
A．[
2
9
，
1
3
] B．[
2
27
，
1
9
] C．[
8
27
，
1
3
] D．[
8
9
，
25
27
]
组卷：23引用：3难度：0.5
解析
5．设a,b∈R，则“a²+b²≥2”是“a+b≥2”的（　　）
A．充要条件 B．必要不充分条件
C．充分不必要条件 D．既不充分也不必要条件
组卷：78引用：1难度：0.7
解析
6．已知函数y=f（x）的定义域是[-8，1]，则函数g（x）=
f
（
2
x
+
1
）
x
+
2
的定义域是（　　）
A．（-∞，-2）∪（-2，3] B．[-8，-2）∪（-2，1]
C．[-
9
2
，-2）∪（-2，0] D．[-
9
2
，-2]
组卷：5052引用：31难度：0.9
解析
7．已知函数
f
（
x
）
=
-
x
2
+
2
ax
+
4
，
x
≤
1
，
1
x
，
x
＞
1
是
[
-
1
2
，
+
∞
）
上的减函数，则a的取值范围是（　　）
A．
[
-
1
，-
1
2
]
B．（-∞，-1] C．
[
-
1
，-
1
2
）
D．（-∞，-1）
组卷：918引用：4难度：0.6
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

四．解答题（本题共6道小题，共70分，解答题应写出文字说明，证明过程或演算步骤）

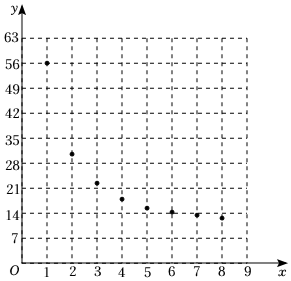21．某企业新研发了一种产品，产品的成本由原料成本及非原料成本组成．每件产品的非原料成本y（元）与生产该产品的数量x（千件）有关，经统计得到如表格数据：

x 1 2 3 4 5 6 7 8

y 56.5 31 22.75 17.8 15.95 14.5 13 12.5

根据以上数据绘制了散点图，观察散点图，两个变量间关系考虑用反比例函数模型
y
=
a
+
b
x
和指数函数模型y=ce^dx分别对两个变量的关系进行拟合．已求得用指数函数模型拟合的回归方程为y=48.376e^-0.195x，lny与x的相关系数r₁=-0.929．
（1）用反比例函数模型求y关于x的回归方程；
（2）用相关系数判断上述两个模型哪一个拟合效果更好（精确到0.001），并用其估计产量为10千件时每件产品的非原料成本；
（3）根据企业长期研究表明，非原料成本y服从正态分布N（μ，σ²），用样本平均数
y
作为μ的估计值
̂
μ
，用样本标准差s作为σ的估计值
̂
σ
，若非原料成本y在μ-σ，μ+σ之外，说明该成本异常，并称落在（μ-σ，μ+σ）之外的成本为异样成本，此时需寻找出现异样成本的原因．利用估计值判断上述非原料成本数据是否需要寻找出现异样成本的原因？
参考数据（其中
u
i
=
1
x
i
）；

u

u
2

8
∑
i
=
1
u
2
i

8
∑
i
=
1
y_i
8
∑
i
=
1
y
2
i

8
∑
i
=
1
u_iy_i
0
.
61
×
1545
.
555

193
.
194

0.34 0.115 1.53 184 5777.555 93.06 30.705 13.9

参考公式：对于一组数据（x₁，y₁），（x₂，y₂），…，（x_n，y_n），其回归直线
̂
y
=
̂
a
+
̂
b
x
的斜率和截距的最小二乘估计公式分别为：
̂
b
=
n
∑
i
=
1
x
i
y
i
-
n
x
•
y
n
∑
i
=
1
x
2
i
-
n
x
2
，
̂
a
=
y
-
̂
b
x
，相关系数
r
=
n
∑
i
=
1
（
x
i
-
x
）
（
y
i
-
y
）
n
∑
i
=
1
（
x
i
-
x
）
2
n
∑
i
=
1
（
y
i
-
y
）
2
．

组卷：53引用：1难度：0.7

解析

22．已知函数f（x）=lnx-a²x²-ax+a-1（a∈R）．
（1）试讨论f（x）的单调性；
（2）若不等式
f
（
x
+
1
）
+
a
2
（
x
+
1
）
2
+
e
x
x
+
1
≥
0
对任意的x≥0恒成立，求实数a的取值范围．
组卷：184引用：4难度：0.2
解析

0/60 进入组卷

0/20 进入试卷篮

布置作业 发布测评 反向细目表 平行组卷 下载答题卡 试卷分析 在线训练 收藏试卷

充值会员，资源免费下载

A．[1，5]	B．（1，5]
C．{0，1，2，3，4，5}	D．{2，3，4，5}

A．∃x₀＜0，使得x₀+1≤0	B．∃x₀≥0，使得x₀+1＞0
C．∀x＜0，都有x+1≤0	D．∀x≥0，都有x+1＞0

A．若a＞b＞0，则ac²＞bc²	B．若a＜b＜0，则 1 a ＜ 1 b
C．若a＜b＜0，则a²＜ab＜b²	D．若a＞b＞0，则a²＞b²

A．充要条件	B．必要不充分条件
C．充分不必要条件	D．既不充分也不必要条件

A．（-∞，-2）∪（-2，3]	B．[-8，-2）∪（-2，1]
C．[- 9 2 ，-2）∪（-2，0]	D．[- 9 2 ，-2]

u	u 2	8 ∑ i = 1 u 2 i	8 ∑ i = 1 y_i	8 ∑ i = 1 y 2 i	8 ∑ i = 1 u_iy_i	0 . 61 × 1545 . 555	193 . 194
0.34	0.115	1.53	184	5777.555	93.06	30.705	13.9

2023年黑龙江省佳木斯一中高考数学第一次调研试卷

一．单选题（本题共8道小题，每题5分，共40分）

1．A={x||x|≥1}，B={x|x-5x-1≤0，x∈N}，则A∩B=（ ）

2．设命题p：∃x0＜0，使得x0+1＞0，则￢p为（ ）

3．下列命题为真命题的是（ ）

5．设a,b∈R，则“a2+b2≥2”是“a+b≥2”的（ ）

6．已知函数y=f（x）的定义域是[-8，1]，则函数g（x）=f（2x+1）x+2的定义域是（ ）

7．已知函数f（x）=-x2+2ax+4，x≤1，1x，x＞1是[-12，+∞）上的减函数，则a的取值范围是（ ）

四．解答题（本题共6道小题，共70分，解答题应写出文字说明，证明过程或演算步骤）

22．已知函数f（x）=lnx-a2x2-ax+a-1（a∈R）．（1）试讨论f（x）的单调性；（2）若不等式f（x+1）+a2（x+1）2+exx+1≥0对任意的x≥0恒成立，求实数a的取值范围．

1．
A
=
{
x
|
|
x
|
≥
1
}
，
B
=
{
x
|
x
-
5
x
-
1
≤
0
，
x
∈
N
}
，则A∩B=（　　）

2．设命题p：∃x₀＜0，使得x₀+1＞0，则￢p为（　　）

3．下列命题为真命题的是（　　）

5．设a,b∈R，则“a²+b²≥2”是“a+b≥2”的（　　）

6．已知函数y=f（x）的定义域是[-8，1]，则函数g（x）=
f
（
2
x
+
1
）
x
+
2
的定义域是（　　）

7．已知函数
f
（
x
）
=
-
x
2
+
2
ax
+
4
，
x
≤
1
，
1
x
，
x
＞
1
是
[
-
1
2
，
+
∞
）
上的减函数，则a的取值范围是（　　）

22．已知函数f（x）=lnx-a²x²-ax+a-1（a∈R）．
（1）试讨论f（x）的单调性；
（2）若不等式
f
（
x
+
1
）
+
a
2
（
x
+
1
）
2
+
e
x
x
+
1
≥
0
对任意的x≥0恒成立，求实数a的取值范围．