2021-2022学年天津市复兴中学高三（上）第二次月考数学试卷

一、单选题（本大题共12小题，共60分。在每小题列出的选项中，选出符合题目的一项）

• 1．定义集合运算：A*B={z|z=xy,x∈A∩B，y∈A∪B}．若集合A={1，2，3}，B={0，1，2}，则∁_（A*B）A=（　　）

  A．{0}

  B．{0，4}

  C．{0，6}

  D．{0，4，6}
  组卷：83引用：5难度：0.8

  解析

• 2．“

  α

  =

  π

  6

  ”是“

  sinα

  =

  1

  2

  ”的（　　）条件．

  A．充分不必要	B．必要不充分
  C．充要	D．既不充分也不必要
  组卷：792引用：15难度：0.9

  解析

• 3．函数y=

  2

  -

  ln

  x

  2

  2

  +

  ln

  x

  2

  sinx,x∈[-e,e]的图象大致为（　　）

  A．

  B．

  C．

  D．
  组卷：356引用：4难度：0.8

  解析

• 4．根据下表中的数据可以得到线性回归直线方程

  ̂

  y

  =0.7x+0.35，则实数m,n应满足（　　）

  x	3	m	5	6
  y	2.5	3	4	n

  A．n-0.7m=1.7

  B．n-0.7m=1.5

  C．n+0.7m=1.7

  D．n+0.7m=1.5
  组卷：588引用：8难度：0.8

  解析

• 5．在等差数列{a_n}中，a₁₀＜0，a₁₁＞0，且a₁₁＞|a₁₀|，则在S_n＜0中，n的最大值为（　　）

  A．17

  B．18

  C．19

  D．20
  组卷：499引用：6难度：0.7

  解析

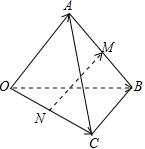• 6．三棱锥O-ABC中，M，N分别是AB，OC的中点，且

  OA

  =

  a

  ，

  OB

  =

  b

  ，

  OC

  =

  c

  ，用

  a

  ，

  b

  ，

  c

  表示

  NM

  ，则

  NM

  等于（　　）

  A． 1 2 （- a + b + c ）

  B． 1 2 （ a + b - c ）

  C． 1 2 （ a - b + c ）

  D． 1 2 （- a - b + c ）
  组卷：2292引用：19难度：0.9

  解析

• 7．已知双曲线

  x

  2

  a

  2

  -

  y

  2

  b

  2

  =1（a＞0，b＞0）的一条渐近线过点（2，

  3

  ），且双曲线的一个焦点在抛物线y²=4

  7

  x的准线上，则双曲线的方程为（　　）

  A． x 2 21 - y 2 28 = 1	B． x 2 28 - y 2 21 =1
  C． x 2 3 - y 2 4 = 1	D． x 2 4 - y 2 3 = 1
  组卷：890引用：13难度：0.9

  解析

三、解答题（本大题共5小题，共60分。解答应写出文字说明，证明过程或演算步骤）

• 22．已知正项数列{a_n}满足

  a

  1

  =

  1

  ，

  a

  2

  n

  +

  1

  -

  （

  2

  n

  +

  1

  ）

  a

  n

  +

  1

  =

  a

  2

  n

  +

  （

  2

  n

  +

  1

  ）

  a

  n

  ．
  （1）求数列{a_n}的通项公式；
  （2）设数列

  {

  1

  a

  n

  }

  的前n项和为T_n，证明：T_n＜2．
  组卷：178引用：3难度：0.6

  解析

• 23．已知数列{a_n}的前n项和为S_n，满足S_n=2a_n-1，n∈N*．数列{b_n}满足nb_n+1-（n+1）b_n=n（n+1），n∈N*，且b₁=1．
  （1）求数列{a_n}和{b_n}的通项公式；
  （2）若c_n=a_n

  •

  b

  n

  ，数列{c_n}的前n项和为T_n，对任意的n∈N*，都有T_n＜nS_n-a,求实数a的取值范围；
  （3）是否存在正整数m,n使b₁，a_m，b_n（n＞1）成等差数列，若存在，求出所有满足条件的m,n,若不存在，请说明理由．
  组卷：167引用：6难度：0.5

  解析