2023-2024学年江苏省徐州市部分学校高三（上）期初数学试卷（9月份）

一、单选题

• 1．已知集合M={y|y=x-|x|，x∈R}，N={y|y=（

  1

  3

  ）^x，x∈R}，则（　　）

  A．M=N

  B．N⊆M

  C．M=∁RN

  D．∁R（N∪M）
  组卷：36引用：1难度：0.7

  解析

• 2．“Z=

  1

  sinθ

  +

  cosθ

  •

  i

  -

  1

  2

  （其中i是虚数单位）是纯虚数．”是“θ=

  π

  6

  +2kπ”的（　　）条件．

  A．充分不必要	B．必要不充分
  C．充要	D．既不充分也不必要
  组卷：30引用：2难度：0.9

  解析

• 3．在正方体ABCD-A₁B₁C₁D₁中，E，F，G分别为AA₁，BC，C₁D₁的中点，现有下面三个结论：①△EFG为正三角形；②异面直线A₁G与C₁F所成角为60°，③AC∥平面EFG；④过A作平面α，使得棱AD，AA₁，D₁C₁在平面α的正投影的长度相等，则这样的平面α有4个．其中所有正确结论的编号是（　　）

  A．②④

  B．②③

  C．①③

  D．①③④
  组卷：25引用：2难度：0.5

  解析

• 4．下列向量的线性运算正确的是（　　）

  A． AB + AC = BC

  B． AB + CB = AC

  C． AB - CB = AC

  D． AB - AC = BC
  组卷：61引用：3难度：0.8

  解析

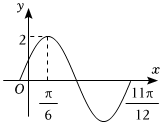• 5．函数y=2sin（ωx+φ）（ω＞0，0＜φ＜π）的部分图象如图所示．则f（π）=（　　）

  A．1

  B． 1 2

  C． 3 2

  D．2
  组卷：381引用：2难度：0.6

  解析

• 6．设f（x）是可导函数，且满足

  lim

  △

  x

  →

  0

  f

  （

  1

  ）

  -

  f

  （

  1

  +

  △

  x

  ）

  2

  △

  x

  =

  2

  ，则曲线y=f（x）在点（1，f（1））处的切线斜率为（　　）

  A．4

  B．-1

  C．1

  D．-4
  组卷：148引用：3难度：0.7

  解析

• 7．若不等式x²+ax+1≥0对于一切x∈（0，

  1

  2

  ）恒成立，则a的取值范围是（　　）

  A．a≥0

  B．a≥-2

  C．a≥- 5 2

  D．a≥-3
  组卷：168引用：6难度：0.5

  解析

五、解答题

• 21．设数列{a_n}的前n项和为S_n，且S_n=2a_n-2ⁿ⁺¹，n∈N^*．
  （1）求数列{a_n}的通项公式；
  （2）令b_n=

  a

  n

  n

  +

  1

  -

  n

  +

  1

  a

  n

  ，记数列

  {

  1

  b

  n

  }

  的前n项和为T_n．求证：T_n＜

  4

  3

  ，n∈N^*．
  组卷：49引用：1难度：0.5

  解析

• 22．设函数

  f

  （

  x

  ）

  =

  x

  -

  2

  x

  -

  a

  （

  lnx

  -

  1

  x

  2

  ）

  ，a∈R．
  （1）讨论f（x）的单调性；
  （2）当a＞0时，记f（x）的最小值为g（a），证明：g（a）＜1．
  组卷：212引用：10难度：0.3

  解析