当前位置：试卷中心 > 试卷详情

2023年浙江省宁波市海曙区兴宁中学中考数学三模试卷

发布：2024/6/13 8:0:9

一、选择题（每小题4分，共40分）

1．2023的相反数是（　　）
A．
1
2023
B．
-
1
2023
C．2023 D．-2023
组卷：5352引用：291难度：0.8
解析
2．下列各式中，计算正确的是（　　）
A．x³+x²=x⁵ B．x³•x²=x⁶ C．x³÷x²=x D．（x³）²=x⁹
组卷：755引用：12难度：0.7
解析
3．2022年10月12日，“天宫课堂”第三课在中国空间站开讲，3名航天员演示了在微重力环境下毛细效应实验、水球变“懒”实验等，相应视频在某短视频平台的点赞量达到150万次，数据150万用科学记数法表示为（　　）
A．1.5×10⁵ B．0.15×10⁵ C．1.5×10⁶ D．1.5×10⁷
组卷：1400引用：24难度：0.7
解析
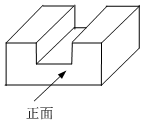4．如图所示的钢块零件的主视图为（　　）
A． B． C． D．
组卷：1493引用：29难度：0.8
解析
5．为深入实施《全民科学素质行动规划纲要（2022—2035年）》，《山西省全民科学素质行动规划纲要实施方案（2021—2025年）》，某校举行了科学素质知识竞赛，进入决赛的学生共有10名，他们的决赛成绩如表所示：

决赛成绩/分 100 95 90 85

人数/名 1 4 2 3

则这10名学生决赛成绩的中位数和众数分别是（　　）
A．92.5，95 B．95，95 C．92.5，93 D．92.5，100
组卷：177引用：4难度：0.8
解析
6．如图已知扇形AOB的半径为6cm,圆心角的度数为120°，若将此扇形围成一个圆锥的侧面，则围成的圆锥的底面积为（　　）
A．4πcm² B．6πcm² C．9πcm² D．12πcm²
组卷：1408引用：12难度：0.9
解析
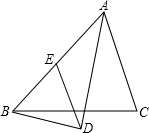7．如图，在△ABC中，AD平分∠BAC，BD⊥AD，垂足为D，过点D作DE∥AC，交AB于E，若AB=5，则线段DE的长为（　　）
A．2 B．
5
2
C．3 D．
7
2
组卷：762引用：4难度：0.5
解析
8．明代《算法统宗》有一首饮酒数学诗：“醇酒一瓶醉三客，薄酒三瓶醉一人，共同饮了一十九，三十三客醉颜生，试问高明能算士，几多醨酒几多醇？”这首诗是说：“好酒一瓶，可以醉倒3位客人；薄酒三瓶，可以醉倒1位客人，如今33位客人醉倒了，他们总共饮19瓶酒．试问：其中好酒、薄酒分别是多少瓶？”设有好酒x瓶，薄酒y瓶．根据题意，可列方程组为（　　）
A．
x
+
y
=
19
3
x
+
1
3
y
=
33
B．
x
+
y
=
19
x
+
3
y
=
33
C．
x
+
y
=
19
1
3
x
+
3
y
=
33
D．
x
+
y
=
19
3
x
+
y
=
33
组卷：2033引用：10难度：0.7
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

三、解答题（第17，18，19题各8分，第20，21，22题各10分，第23题12分，第24题14分，共80分，解答应写出证明过程或演算步骤）

23．点C在AB的延长线上，且∠DAB=∠DBE，

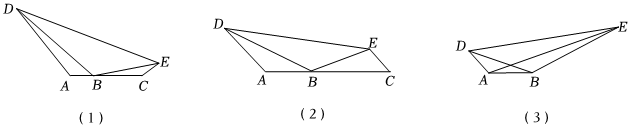
【证明体验】
（1）如图（1），若∠C=∠A，求证：△DAB∽△BCE；
【思考探究】
（2）如图（2），若CE∥AD，∠C=45°，若
AD
=
2
AB
，求
CE
BC
的值；
【拓展延伸】
（3）如图（3），连接AE，若△DAB∽△DBE，
AB
AD
=
2
，若AE=nBD，求n的值．
组卷：463引用：1难度：0.3
解析
24．如图1，在菱形ABCD中，
AB
=
2
5
，点P是对角线BD上的动点，⊙O是△PAB的外接圆，tan
∠
DBC
=
1
2
，设⊙O的半径为r,BP=x.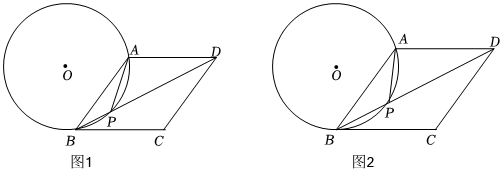

（1）如图2，当PA=PB时，求证：BC是⊙O切线；
（2）延长AP交射线BC于点Q．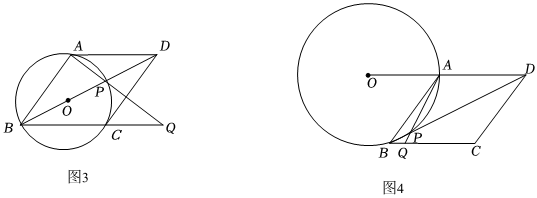

①如图3，若BP为⊙O直径，求CQ的长；
②如图4，若点O、A、D三点共线，求
AP
PQ
的值；
（3）当0＜x＜4时，直接写出r与x的函数关系式：
．
组卷：253引用：1难度：0.4
解析