当前位置：试卷中心 > 试卷详情

2023-2024学年北京理工大学附中高二（上）月考数学试卷（10月份）

发布：2024/9/17 9:0:8

1．若点A在直线b上，b在平面β内，则A，b,β之间的关系可以记作（　　）
A．A∈b∈β B．A⊂b⊂β C．A∈b⊂β D．A⊂b∈β
组卷：95引用：3难度：0.9
解析
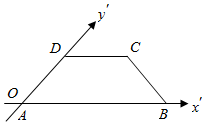2．如图，一个水平放置的平面图形的直观图（斜二测画法）是一个底角为45°、腰和上底长均为2的等腰梯形，则这个平面图形的面积是（　　）
A．
2
+
2
B．
1
+
2
C．
4
+
2
2
D．
8
+
4
2
组卷：216引用：7难度：0.9
解析
3．已知圆锥的底面半径为1，且它的侧面展开图是一个半圆，则这个圆锥的体积为（　　）
A．
3
3
π
B．
3
π
C．
5
3
π
D．
5
π
组卷：185引用：10难度：0.9
解析
4．已知平面α∥平面β，过平面α内的一条直线a的平面γ，与平面β相交，交线为直线b,则a、b的位置关系是（　　）
A．平行 B．相交 C．异面 D．不确定
组卷：98引用：3难度：0.8
解析
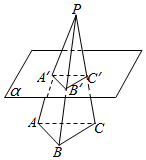5．已知P为△ABC所在平面外一点，平面α∥平面ABC，且α交线段PA，PB，PC于点A′，B′，C′，若PA′：AA′=2：3，则S_{△A′B′C′}：S_△ABC=（　　）
A．2：3 B．2：5 C．4：9 D．4：25
组卷：1454引用：10难度：0.9
解析
6．已知正方体ABCD-A₁B₁C₁D₁中，点E为上底面A₁C₁的中心，若
AE
=
A
A
1
+x
AB
+y
AD
，则x,y的值分别为（　　）
A．1，1 B．1，
1
2
C．
1
2
，
1
2
D．
1
2
，1
组卷：307引用：14难度：0.9
解析

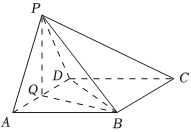18．如图示，正方形ABCD与正三角形ADP所在平面互相垂直，Q是AD的中点．
（1）求证：PQ⊥BQ；
（2）在线段AB上是否存在一点N，使面PCN⊥面PQB？并证明你的结论．
组卷：264引用：2难度：0.5
解析
19．如图，四边形ABCD中，AB⊥AD，AD∥BC，AD=6，BC=2AB=4，E，F分别在BC，AD上，EF∥AB，现将四边形ABCD沿EF折起，使BE⊥EC．

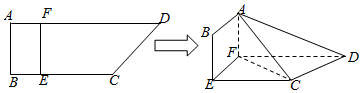
（1）若BE=1，在折叠后的线段AD上是否存在一点P，使得CP∥平面ABEF？若存在，求出
AP
PD
的值；若不存在，说明理由．
（2）求三棱锥A-CDF的体积的最大值，并求出此时点F到平面ACD的距离．
组卷：166引用：7难度：0.3
解析

1．若点A在直线b上，b在平面β内，则A，b,β之间的关系可以记作（ ）