2022-2023学年江西省赣州市上犹中学高一（下）期末数学试卷

一、单选题（每题5分，共40分）

• 1．若集合A={x∈N|-2＜x＜1}，B={-2，-1，0，1}，则A∩B=（　　）

  A．∅

  B．{-1}

  C．{0}

  D．{-1，0}
  组卷：397引用：11难度：0.9

  解析

• 2．已知角的顶点与直角坐标系的原点重合，始边与x轴的非负半轴重合，那么，下列各角与380°角终边相同的是（　　）

  A．20°

  B．30°

  C．40°

  D．50°
  组卷：139引用：3难度：0.8

  解析

• 3．已知向量

  a

  =

  （

  2

  ，

  1

  ）

  ，

  b

  =

  （

  m

  ,

  1

  ）

  ，若

  a

  ⊥

  b

  ，则m为（　　）

  A．1

  B． 1 2

  C．0

  D． - 1 2
  组卷：62引用：3难度：0.8

  解析

• 4．设向量

  a

  ，

  b

  不平行，向量

  λ

  a

  +

  b

  与

  a

  +

  2

  b

  平行，则实数λ为（　　）

  A． 1 2

  B．1

  C．2

  D．-1
  组卷：248引用：4难度：0.7

  解析

• 5．已知平面向量

  a

  ，

  b

  满足

  a

  =

  （

  1

  ，-

  3

  ）

  ，

  |

  b

  |

  =

  1

  ，

  |

  a

  +

  2

  b

  |

  =

  2

  ，则向量

  a

  与向量

  b

  的夹角为（　　）

  A． π 6

  B． π 4

  C． π 3

  D． 2 π 3
  组卷：444引用：5难度：0.8

  解析

• 6．已知长方体的长、宽、高分别为1，1，2，并且其顶点都在球O的球面上，则球O的体积是（　　）

  A． 2 π

  B． 6 π

  C． 2 2 π

  D．6π
  组卷：157引用：3难度：0.8

  解析

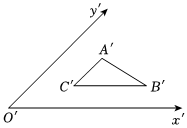• 7．如图所示是利用斜二测画法画出的水平放置的△ABC的直观图，已知A′C′∥y′轴，B′C′∥x′轴且2A′C′=B′C′=2，则△ABC的周长为（　　）

  A． 4 + 2 2

  B． 2 + 2 2

  C． 2 + 2 3

  D． 4 + 3
  组卷：134引用：5难度：0.7

  解析

四、解答题（共70分）

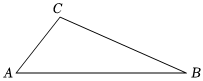• 21．如图，设A，B是海岸线相距

  （

  15

  2

  +

  5

  6

  ）

  nmile的两个观察所，一渔轮在C处遇险，发出求救信号，两观察所同时收到求救信号，收到求救信号时，测得∠CAB=45°，∠ABC=15°，并发现渔轮正在以9nmile/h的速度向观察所B行驶，若观察所A，B的救援舰艇的最高速度都是21nmile/h.试判断从何处派遣救援舰艇更合理，请说明理由并说出具体救援路线．（参考数据：

  sin

  21

  ．

  8

  °≈

  3

  14

  3

  ）
  组卷：7引用：2难度：0.5

  解析

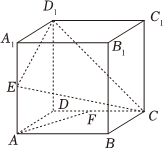• 22．在直四棱柱ABCD-A₁B₁C₁D₁中，E，F分别是AA₁，DC的中点．
  （1）求证：AF∥平面CED₁；
  （2）若AD⊥DC，AD=DC=1，AA₁=2，求点F到平面CED₁的距离；
  （3）B是否在平面CED₁上，回答是与否，不需要说明理由．
  组卷：15引用：3难度：0.5

  解析