2022-2023学年湖北省重点中学4G联合体高二（上）期中数学试卷

一、选择题（共8小题，每小题5分，满分40分）

• 1．已知点

  A

  （

  0

  ，

  3

  ）

  ，点

  B

  （

  -

  1

  ，

  2

  3

  ）

  ，则直线AB的倾斜角为（　　）

  A．150°

  B．120°

  C．45°

  D．30°
  组卷：30引用：7难度：0.9

  解析

• 2．如图，在斜棱柱ABCD-A₁B₁C₁D₁中，AC与BD的交点为点M，

  AB

  =

  a

  ，

  AD

  =

  b

  ，

  A

  A

  1

  =

  c

  ，则

  M

  C

  1

  =（　　）

  A． 1 2 a + 1 2 b + c

  B． - 1 2 a - 1 2 b - c

  C． - 1 2 a + 1 2 b + c

  D． - 1 2 a - 1 2 b + c
  组卷：1435引用：24难度：0.8

  解析

• 3．在一些山谷中有一种奇特的现象，在一处呼喊一声，在另一处会间隔听到两次呼喊，前一次是声音直接传到听者耳朵中，后一次是声音经过山壁反射后再传到听者耳朵中．假设有一片椭圆形状的空旷山谷，甲、乙两人分别站在椭圆的两个焦点处，甲呼喊一声，乙经过2s听到第一声，又过4s听到第二声，则该椭圆的离心率为（　　）

  A． 1 3

  B． 1 2

  C． 2 3

  D． 3 3
  组卷：14引用：2难度：0.6

  解析

• 4．已知空间内三点A（1，0，2），B（-1，2，0），C（0，3，1），则点A到直线BC的距离是（　　）

  A． 4 6 3

  B． 4 3

  C． 6 3

  D． 2 3 3
  组卷：768引用：7难度：0.7

  解析

• 5．若直线y=kx+1与圆x²+y²+kx+my-4=0交于M，N两点，且M，N关于直线x+2y=0对称，则实数k+m的值为（　　）

  A．1

  B．2

  C．3

  D．0
  组卷：132引用：5难度：0.7

  解析

• 6．由2个人在一座8层大楼的底层进入电梯，假设每一个人自第二层开始在每一层离开电梯是等可能的，则这两个人在不同层离开电梯的概率是（　　）

  A． 7 8

  B． 6 7

  C． 5 6

  D． 36 49
  组卷：54引用：3难度：0.9

  解析

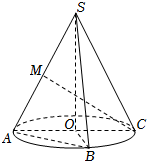• 7．如图，某圆锥SO的轴截面SAC，其中SA=

  5

  AO，点B是底面圆周上的一点，且cos∠BOC=

  2

  3

  ，点M是线段SA的中点，则异面直线SB与CM所成角的余弦值是（　　）

  A． 2 35 35

  B． 6 65 65

  C． 13 15

  D． 3 5
  组卷：120引用：5难度：0.6

  解析

四、解答题（共6小题，满分70分）

• 21．在四棱锥P-ABCD中，底面ABCD为直角梯形，AD∥BC，AD⊥AB，侧面PAB⊥底面ABCD，PA=PB=AD=

  1

  2

  BC=2，且E，F分别为PC，CD的中点．
  （1）证明：DE∥平面PAB；
  （2）若直线PF与平面PAB所成的角为60°，求平面PAB与平面PCD所成锐二面角的余弦值．
  组卷：284引用：26难度：0.6

  解析

• 22．已知A，B是椭圆

  C

  ：

  x

  2

  a

  2

  +

  y

  2

  b

  2

  =

  1

  （

  a

  ＞

  b

  ＞

  0

  ）

  的左、右顶点，且短轴长为2，M是椭圆C上位于x轴上方的动点，且直线AM的斜率与直线BM的斜率之积为

  -

  1

  4

  ．
  （1）求椭圆C的方程；
  （2）若直线AM，BM与直线l：x=4分别交于C，D两点，记△MAB和△MCD的面积分别为S₁和S₂.求

  S

  1

  S

  2

  的取值范围．
  组卷：27引用：2难度：0.5

  解析