2022-2023学年北京市丰台区高二（下）期末数学试卷

一、选择题共10小题，每小题4分，共40分。在每小题列出的四个选项中，选出符合题目要求的一项。

• 1．在等差数列{a_n}中，a₁=1，a_n-a_n-1=2（n≥2），则a₆=（　　）

  A．10

  B．11

  C．12

  D．13
  组卷：263引用：2难度：0.8

  解析

• 2．已知

  P

  （

  A

  ）

  =

  1

  2

  ，

  P

  （

  AB

  ）

  =

  1

  3

  ，那么P（B|A）=（　　）

  A． 1 6

  B． 1 3

  C． 2 3

  D． 5 6
  组卷：199引用：2难度：0.8

  解析

• 3．如图所示的三角形图案是谢尔宾斯基三角形．已知第n个图案中黑色与白色三角形的个数之和为a_n，数列{a_n}满足a₁=1，a_n+1=3a_n+1（n≥1），那么下面各数中是数列{a_n}中的项的是（　　）
  

  A．121

  B．122

  C．123

  D．124
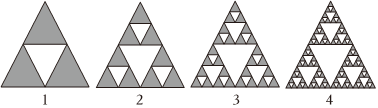  组卷：175引用：3难度：0.5

  解析

• 4．已知某生物技术公司研制出一种新药，并进行了临床试验，该临床试验的成功概率是失败概率的2倍．若记一次试验中成功的次数为X，则随机变量X的数学期望为（　　）

  A． 2 3

  B． 1 2

  C． 1 3

  D． 1 6
  组卷：197引用：3难度：0.5

  解析

• 5．用充气筒吹气球，气球会鼓起来，假设此时气球是一个标准的球体，且气球的体积V（r）随着气球半径r的增大而增大．当半径r=1时，气球的体积

  V

  （

  r

  ）

  =

  4

  3

  π

  r

  3

  相对于r的瞬时变化率为（　　）

  A． 4 3 π

  B．2π

  C．4π

  D．8π
  组卷：208引用：5难度：0.7

  解析

• 6．某人需要先从A地到B地，再同站转车赶到C地，他能够选择的高铁车次的列车时刻表如下表所示，那么此人这天乘坐高铁列车从A地到C地不同的乘车方案总数为（　　）
  A地至B地高铁列车时刻表
  

  车次	发车时间	到站时间
  G87	07：00	08：01
  G91	07：55	08：56
  G93	09：00	10：01

  B地至C地高铁列车时刻表

  车次	发车时间	到站时间
  G2811	08：25	10：31
  G653	09：24	11：13
  G501	10：26	12：30

  A．9

  B．6

  C．4

  D．3
  组卷：70引用：1难度：0.9

  解析

• 7．正态分布在概率和统计中占有重要地位，它广泛存在于自然现象、生产和生活实践之中．在现实生活中，很多随机变量都服从或近似服从正态分布．假设随机变量X～N（μ，σ²），可以证明，对给定的k∈N^*，P（μ-kσ≤X≤μ+kσ）是一个只与k有关的定值，部分结果如图所示：
  通过对某次数学考试成绩进行统计分析，发现考生的成绩ξ基本服从正态分布ξ～N（105，10²）．若共有1000名考生参加这次考试，则考试成绩在（105，125）的考生人数大约为（　　）

  A．341

  B．477

  C．498

  D．683
  组卷：191引用：2难度：0.7

  解析

三、解答题共6小题，共85分。解答应写出文字说明，演算步骤或证明过程。

• 20．已知函数f（x）=e^x-ax-1（a∈R）．
  （1）求曲线y=f（x）在点（0，f（0））处的切线方程；
  （2）讨论函数f（x）的单调性；
  （3）判断e^0.01与1.01的大小关系，并说明理由．
  组卷：347引用：3难度：0.4

  解析

• 21．正实数构成的集合A={a₁，a₂，⋯，a_n}（n≥2），定义A⊗A={a_i•a_j|a_i，a_j∈A，且i≠j}．当集合A⊗A中的元素恰有

  n

  （

  n

  -

  1

  ）

  2

  个数时，称集合A具有性质Ω．
  （Ⅰ）判断集合A₁={1，2，4}，A₂={1，2，4，8}是否具有性质Ω；
  （Ⅱ）若集合A具有性质Ω，且A中所有元素能构成等比数列，A⊗A中所有元素也能构成等比数列，求集合A中的元素个数的最大值；
  （Ⅲ）若集合A具有性质Ω，且A⊗A中的所有元素能构成等比数列．问：集合A中的元素个数是否存在最大值？若存在，求出该最大值；若不存在，请说明理由．
  组卷：65引用：3难度：0.2

  解析