2023-2024学年山东省潍坊市昌乐二中八年级（上）月考数学试卷（10月份）

一、选择题

• 1．下列说法不正确的是（　　）

  A．等腰三角形是轴对称图形

  B．三角相等的三角形是等边三角形

  C．如果两个三角形成轴对称，那么这两个三角形一定全等

  D．若A，B两点关于直线MN对称，则AB垂直平分MN
  组卷：12引用：2难度：0.8

  解析

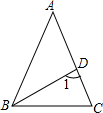• 2．如图，在△ABC中，AB=AC，BD平分∠ABC，若∠A=52°，则∠1的度数为（　　）

  A．64°

  B．78°

  C．84°

  D．88°
  组卷：365引用：4难度：0.9

  解析

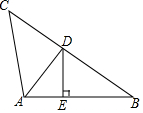• 3．如图，AD是△ABC中∠BAC的角平分线，DE⊥AB于点E，S_△ABC=7，DE=2，AB=4，则AC长是（　　）

  A．3

  B．4

  C．6

  D．5
  组卷：2849引用：41难度：0.7

  解析

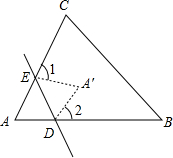• 4．如图，△ABC中，点D，E分别在边AB，AC上，将∠A沿着DE所在直线折叠，A与A′重合，若∠1+∠2=140°，则∠A的度数是（　　）

  A．70°

  B．75°

  C．80°

  D．85°
  组卷：564引用：5难度：0.5

  解析

• 5．如图，已知∠O，点P为其内一定点，分别在∠O的两边上找点A、B，使△PAB周长最小的是（　　）

  A．

  B．

  C．

  D．
  组卷：3704引用：25难度：0.8

  解析

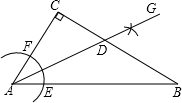• 6．如图，在△ABC中，∠C=90°，∠CAB=50°，按以下步骤作图：
  ①以点A为圆心，小于AC长为半径画弧，分别交AB、AC于点E、F；
  ②分别以点E、F为圆心，大于

  1

  2

  EF长为半径画弧，两弧相交于点G；
  ③作射线AG，交BC边于点D．
  则∠ADC的度数为（　　）

  A．40°

  B．55°

  C．65°

  D．75°
  组卷：4334引用：29难度：0.9

  解析

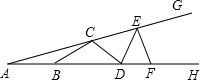• 7．如图，C、E和B、D、F分别在∠GAH的两边上，且AB=BC=CD=DE=EF，若∠A=18°，则∠GEF的度数是（　　）

  A．80°

  B．90°

  C．100°

  D．108°
  组卷：368引用：7难度：0.9

  解析

四、解答题

• 22．如图，在等腰△ABC中，AB=AC，D为底边BC延长线上任意一点，过点D作DE∥AB，与AC延长线交于点E．
  （1）则△CDE的形状是

  ；
  （2）若在AC上截取AF=CE，连接FB、FD，判断FB、FD的数量关系，并给出证明．
  组卷：1626引用：7难度：0.6

  解析

• 23．已知，在等边三角形ABC中，点E在AB上，点D在CB的延长线上，且ED=EC．
  （1）【特殊情况，探索结论】
  如图1，当点E为AB的中点时，确定线段AE与DB的大小关系，请你直接写出结论：AE

  DB（填“＞”、“＜”或“=”）．
  （2）【特例启发，解答题目】
  如图2，当点E为AB边上任意一点时，确定线段AE与DB的大小关系，并说明理由．（提示：过点E作EF∥BC，交AC于点F）
  （3）【拓展结论，设计新题】
  在等边三角形ABC中，点E在直线AB上，点D在线段CB的延长线上，且ED=EC，若△ABC的边长为1，AE=2，求CD的长（请你画出相应图形，并直接写出结果）．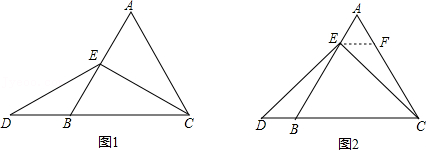
  
  组卷：419引用：12难度：0.3

  解析