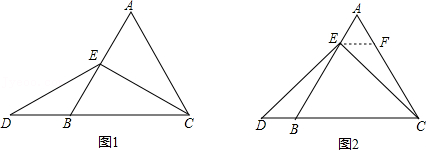
已知，在等边三角形ABC中，点E在AB上，点D在CB的延长线上，且ED=EC．
（1）【特殊情况，探索结论】
如图1，当点E为AB的中点时，确定线段AE与DB的大小关系，请你直接写出结论：AE ==DB（填“＞”、“＜”或“=”）．
（2）【特例启发，解答题目】
如图2，当点E为AB边上任意一点时，确定线段AE与DB的大小关系，并说明理由．（提示：过点E作EF∥BC，交AC于点F）
（3）【拓展结论，设计新题】
在等边三角形ABC中，点E在直线AB上，点D在线段CB的延长线上，且ED=EC，若△ABC的边长为1，AE=2，求CD的长（请你画出相应图形，并直接写出结果）．
【考点】三角形综合题．
【答案】=
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/9/22 16:0:8组卷：419引用：12难度：0.3
相似题
-
1．如图，在△ABC中，∠BAC=90°，以AB为一边向外作正方形ABDE，点F为直线BC上的一点，连接DF，作FG⊥DF交直线AB于点G．
（1）如图1，若AB=AC，点F在线段BC上，请直接写出线段DF与FG的数量关系；
（2）如图2，若AB=AC，点F在线段BC上，试探究线段BD，BF，BG三者之间的数量关系，并证明你的结论；3
（3）若AB=AC，AB=3，DF=23，请直接写出AG的长．2发布：2025/5/25 8:30:2组卷：125引用：1难度：0.2 -
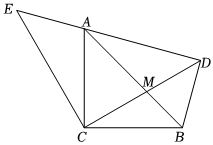2．如图，△ACB和△ECD都是等腰直角三角形，CA=CB，CE=CD，△ACB的顶点A在△ECD的斜边DE上，连接DB．
（1）证明：△EAC≌△DBC；
（2）当点A在线段ED上运动时，猜想AE、AD和AC之间的关系，并证明．
（3）在A的运动过程中，当，AE=2时，求△ACM的面积．AD=6发布：2025/5/25 8:30:2组卷：376引用：5难度：0.1 -
3．【阅读理解】
截长补短法，是初中数学几何题中一种辅助线的添加方法．截长就是在长边上截取一条线段与某一短边相等，补短是通过在一条短边上延长一条线段与另一短边相等，从而解决问题．
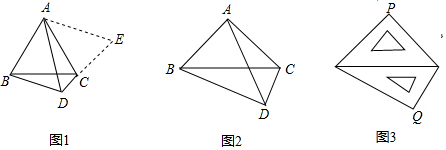
（1）如图1，△ABC是等边三角形，点D是边BC下方一点，∠BDC=120°，探索线段DA、DB、DC之间的数量关系．
解题思路：延长DC到点E，使CE=BD，连接AE，根据∠BAC+∠BDC=180°，可证∠ABD=∠ACE易证得△ABD≌△ACE，得出△ADE是等边三角形，所以AD=DE，从而探寻线段DA、DB、DC之间的数量关系．
根据上述解题思路，请直接写出DA、DB、DC之间的数量关系是 ；
【拓展延伸】
（2）如图2，在Rt△ABC中，∠BAC=90°，AB=AC．若点D是边BC下方一点，∠BDC=90°，探索线段DA、DB、DC之间的数量关系，并说明理由；
【知识应用】
（3）如图3，两块斜边长都为14cm的三角板，把斜边重叠摆放在一起，则两块三角板的直角顶点之间的距离PQ的长为 cm.发布：2025/5/25 9:0:1组卷：427引用：6难度：0.3
