当前位置：试卷中心 > 试卷详情

2023-2024学年江苏省扬州市邗江区汪曾祺学校九年级（上）月考数学试卷（9月份）

发布：2024/8/31 17:0:8

一、选择题（本大题共8小题，共24.0分．）

1．某校运动会前夕，要选60名身高基本相同的女同学组成表演方阵，在这个问题中，最值得关注的是该校所有女生身高的（　　）
A．方差 B．众数 C．平均数 D．中位数
组卷：298引用：6难度：0.8
解析
2．若a是x²-3x-2021=0的一个根，则a²-3a+1的值是（　　）
A．2020 B．2021 C．2022 D．2023
组卷：415引用：3难度：0.7
解析
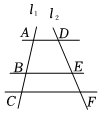3．如图，AD∥BE∥CF，直线l₁、l₂与这三条直线分别交于点A、B、C和D、E、F．若AB=6，BC=3，EF=4，则DE的长为（　　）
A．4 B．6 C．8 D．9
组卷：126引用：3难度：0.6
解析
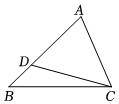4．如图，要使△ABC∽△ACD，需补充的条件不能是（　　）
A．∠ADC=∠ACB B．∠ABC=∠ACD C．
AD
AC
=
AC
AB
D．
AD
DC
=
AC
BC
组卷：353引用：4难度：0.6
解析
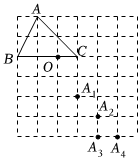5．如图，在6×6的正方形网格中，以O为位似中心，把格点△ABC放大为原来的2倍，则A的对应点为（　　）
A．点A₁ B．点A₂ C．点A₃ D．点A₄
组卷：174引用：5难度：0.7
解析
6．关于x的一元二次方程ax²-2x+1=0有两个不相等实数根，则整数a最大是（　　）
A．2 B．1 C．0 D．-1
组卷：252引用：2难度：0.6
解析
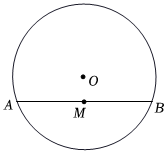7．如图，已知⊙O的直径为26，弦AB=24，动点P、Q在⊙O上，弦PQ=10，若点M、N分别是弦AB、PQ的中点，则线段MN的取值范围是（　　）
A．7≤MN≤17 B．14≤MN≤34 C．7＜MN＜17 D．6≤MN≤16
组卷：1764引用：8难度：0.5
解析
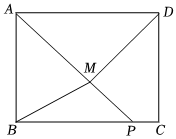8．如图，四边形ABCD为矩形，AB=6，BC=8，点P是线段BC上一动点，DM⊥AP，垂足为M，则BM的最小值为（　　）
A．5 B．
24
5
C．
48
5
D．
2
13
-
4
组卷：375引用：3难度：0.5
解析

二、填空题（本大题共10小题，共30.0分）

9．一组数据：8，-2，-1，5的极差为
．
组卷：82引用：4难度：0.7
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

三、解答题（本大题共10小题，共96.0分）

27．阅读理解：
转化思想是常用的数学思想之一．在研究新问题或复杂问题时，常常把问题转化为熟悉的或比较简单的问题来解决．如解一元二次方程是转化成一元一次方程来解决的；解分式方程是转化为整式方程来解决的．由于“去分母”可能产生增根，所以解分式方程必须检验．
利用转化思想，我们还可以解一些新的方程，如无理方程（根号下含有未知数的方程）．解无理方程关键是要去掉根号，可以将方程适当变形后两边同时平方，将其转化为整式方程．由于“去根号”可能产生增根，所以解无理方程也必须检验．
例如：解方程
x
2
+
12
=2x.
解：两边平方得：x²+12=4x²．
解得：x₁=2，x₂=-2，
经检验，x₁=2是原方程的根，
x₂=-2代入原方程中不合理，是原方程的增根．
∴原方程的根是x=2．
解决问题：
（1）填空：已知关于x的方程
3
x
-
a
=x有一个根是x=1，那么a的值为
；
（2）求满足
x
+
6
=x的x的值；
（3）代数式
x
2
+
9
+
（
8
-
x
）
2
+
9
的值能否等于8？若能，求出x的值；若不能，请说明理由．
组卷：450引用：4难度：0.6
解析
28．定义：在等腰三角形中，若有一条边是另一条边的2倍，则称这个三角形为倍腰三角形．
理解定义：若有一个倍腰三角形有一条边为2，这个倍腰三角形的周长为
．
性质探究：判断下列关于倍腰三角形的说法是否正确，正确的打“√”；错误的打“×”；
（1）所有的倍腰三角形都是相似三角形
．
（2）如图1，依次连接倍腰三角形ABC各边的中点，则图1中共有4个倍腰三角形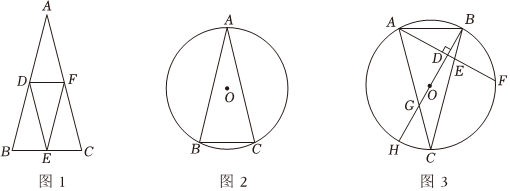
．

性质应用：
（3）如图2，倍腰三角形ABC是⊙O的内接三角形，且AB=AC，若⊙O的半径为1，求倍腰三角形ABC的面积．
拓展应用：
（4）如图3，⊙O是△ABC的外接圆，直径BH⊥AF于点D，AF与BC相交于点E，AC与BH相交于点G，△ABE是倍腰三角形，其中AB=AE，BE=2．请直接写出CG的长．
组卷：81引用：1难度：0.2
解析