2023-2024学年浙江省温州市苍南县六校联考八年级（上）第一次月考数学试卷

一、选择题（本题有10个小题，每小题3分，共30分）

• 1．如图，为了估计一池塘岸边两点A，B之间的距离，小颖同学在池塘一侧选取了一点P，测得PA=100m,PB=90m,那么点A与点B之间的距离可能是（　　）

  A．10m

  B．120m

  C．190m

  D．220m
  组卷：376引用：15难度：0.7

  解析

• 2．下面由北京冬奥会比赛项目图标组成的四个图形中，可看作轴对称图形的是（　　）

  A．

  B．

  C．

  D．
  组卷：828引用：25难度：0.9

  解析

• 3．若不等式-3x＜1，两边同时除以-3，得（　　）

  A．x＞- 1 3

  B．x＜- 1 3

  C．x＞ 1 3

  D．x＜ 1 3
  组卷：663引用：6难度：0.7

  解析

• 4．将一副三角尺按如图的方式摆放，其中l₁∥l₂，则∠α的度数是（　　）

  A．30°

  B．45°

  C．60°

  D．70°
  组卷：1076引用：18难度：0.9

  解析

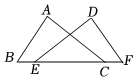• 5．如图，∠A=∠D=90°，AC=DE，使△ABC≌△DFE，需添加一个条件，下列所给的条件及相应的判定定理不正确的是（　　）

  A．AB=DF（SAS）	B．∠B=∠F（AAS）
  C．BC=FE（SSA）	D．∠ACB=∠DEF（ASA）
  组卷：54引用：3难度：0.5

  解析

• 6．给出下列命题：①三角形任何两边之和大于第三边；②三角形任何一外角等于两内角之和；③两边和一角对应相等的两个三角形全等，下列属于真命题的是（　　）

  A．①③

  B．②③

  C．①②

  D．①
  组卷：87引用：3难度：0.6

  解析

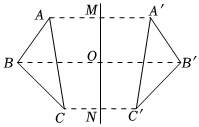• 7．如图，若△ABC与△A′B′C′关于直线MN对称，BB′交MN于点O，则下列说法中不一定正确的是（　　）

  A．AC=A′C′

  B．AB∥B′C′

  C．AA′⊥MN

  D．BO=B′O
  组卷：557引用：37难度：0.9

  解析

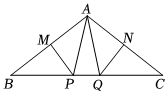• 8．如图，∠BAC=100°，AB＞AC．若MP和NQ分别垂直平分AB和AC，则∠PAQ的度数是（　　）

  A．20°

  B．60°

  C．50°

  D．40°
  组卷：307引用：3难度：0.5

  解析

三、解答题（共46分）

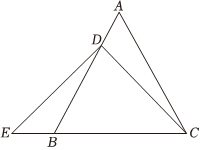• 23．如图，在等边三角形ABC中，D是AB上的一点，E是CB延长线上一点，连接CD、DE，已知∠EDB=∠ACD．
  （1）求证：△DEC是等腰三角形．
  （2）当∠BDC=5∠EDB，EC=8时，求△EDC的面积．
  组卷：3760引用：7难度：0.3

  解析

• 24．问题背景：如图1，在四边形ABCD中，AB=AD，∠BAD=120°，∠B=∠ADC=90°，E，F分别是BC，CD上的点，且∠EAF=60°，探究图中线段BE，EF，FD之间的数量关系，小王同学探究此问题的方法是，延长FD到点G．使DG=BE．连接AG，先证明△ABE≌△ADG，再证明△AEF≌△AGF，可得出结论，他的结论应是

  ；
  探索延伸：如图2，若在四边形ABCD中，AB=AD，∠B+∠D=180°，E，F分别是BC，CD上的点，且∠EAF=

  1

  2

  ∠BAD，上述结论是否仍然成立，并说明理由；
  实际应用：如图3，在某次军事演习中，舰艇甲在指挥中心（O处）北偏西30°的A处，舰艇乙在指挥中心南偏东70°的B处，并且两舰艇到指挥中心的距离相等，接到行动指令后，舰艇甲向正东方向以70海里/小时的速度前进，舰艇乙沿北偏东50°的方向以90海里/小时的速度，前进2小时后，指挥中心观测到甲、乙两舰艇分别到达E，F处，且两舰艇之间的夹角为70°，试求此时两舰艇之间的距离．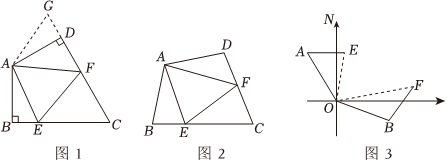
  
  组卷：4983引用：9难度：0.3

  解析