2023-2024学年辽宁省沈阳十一中高二(上)月考数学试卷(10月份)
发布:2024/9/16 3:0:8
一、选择题(本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项符合题目要求)
-
1.已知空间三点A(1,0,3),B(-1,1,4),C(2,-1,3),若
,且|AP∥BC|=AP,则点P的坐标为( )14组卷:460引用:6难度:0.6 -
2.已知点A(2,-1),B(3,m),若m∈[
],则直线AB的倾斜角的取值范围为( )-33-1,3-1组卷:259引用:7难度:0.8 -
3.过点P(1,2)引一条直线,使它与点A(2,3)和点B(4,-5)的距离相等,那么这条直线的方程是( )
组卷:345引用:10难度:0.9 -
4.在平行六面体ABCD-A1B1C1D1中,已知AB=4,AD=3,AA1=5,∠BAD=90°,∠BAA1=∠DAA1=60°,则
的值为( )AC•BD1组卷:87引用:3难度:0.7 -
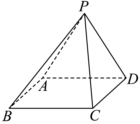 5.如图,四棱锥P-ABCD中,底面ABCD为正方形,△PAD是正三角形,AB=2,平面PAD⊥平面ABCD,则PC与BD所成角的余弦值为( )组卷:199引用:3难度:0.7
5.如图,四棱锥P-ABCD中,底面ABCD为正方形,△PAD是正三角形,AB=2,平面PAD⊥平面ABCD,则PC与BD所成角的余弦值为( )组卷:199引用:3难度:0.7 -
6.已知圆C1:(x+1)2+y2=25,圆C2:(x-1)2+y2=1,动圆M与圆C2外切,同时与圆C1内切,则动圆圆心M的轨迹方程为( )
组卷:183引用:7难度:0.6 -
7.若直线y=kx-1与函数
的图象恰有3个不同的交点,则k的取值范围为( )f(x)=-2x-x2,0≤x≤2-x2+6x-8,2<x≤4组卷:122引用:5难度:0.5
四、解答题(本题共6小题,共70分,解答应写出文字说明、证明过程或演算步骤)
-
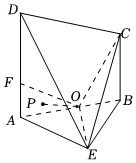 21.如图,DA和CB都垂直于平面ABE,F是DA上一点,且CB=4,AF=2,△ABE为等腰直角三角形,且O是斜边AB的中点,CE与平面ABE所成的角为45°.
21.如图,DA和CB都垂直于平面ABE,F是DA上一点,且CB=4,AF=2,△ABE为等腰直角三角形,且O是斜边AB的中点,CE与平面ABE所成的角为45°.
(1)证明:FO⊥平面OCE;
(2)求二面角F-EC-O的平面角的正切值;
(3)若点P是平面ADE内一点,且OC⊥OP,设点P到平面ABE的距离为d1,PA=d2,求d1+d2的最小值.组卷:974引用:7难度:0.1 -
22.如图(1)所示,在△ABC中,
,AB=43,∠B=60°,DE垂直平分AB.现将三角形ADE沿DE折起,使得二面角A-DE-B大小为60°,得到如图(2)所示的空间几何体(折叠后点A记作点P).BC=23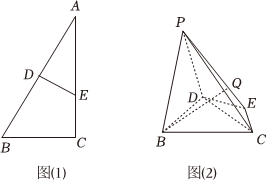
(1)求点D到面PEC的距离;
(2)点Q为一动点,满足,当直线BQ与平面PEC所成角最大时,试确定点Q的位置.PQ=λPE(0<λ<1)组卷:245引用:7难度:0.3


