当前位置：试卷中心 > 试卷详情

2023-2024学年辽宁省大连八中高二（上）月考数学试卷（10月份）

发布：2024/9/22 10:0:8

3．以下四个命题中，正确的是（　　）

A．向量

=（1，-1，3）与向量

=（3，-3，6）平行

B．△ABC为直角三角形的充要条件是

•

C．|（

•

）

c|=|

|•|

D．若{

，

}为空间的一个基底，则{

，

}构成空间的另一个基底

组卷：90引用：11难度：0.5

4．设x,y∈R，向量
a
=
（
0
，
1
，
z
）
，
b
=
（
2
，
y
,
2
）
，
c
=
（
-
3
，
6
，-
3
）
，且
a
⊥
c
，
b
∥
c
，则
|
a
-
b
|
=（　　）
A．
29
B．
2
6
C．3 D．
2
2
组卷：78引用：11难度：0.7
解析
5．过点P（1，3）作直线l,若l经过点A（a,0）和B（0，b），且a,b均为正整数，则这样的直线l可以作出（　　）
A．1条 B．2条 C．3条 D．无数条
组卷：209引用：6难度：0.6
解析
6．数学巨星欧拉（LeonhardEuler,1707～1783）在1765年发表的《三角形的几何学》一书中有这样一个定理：“三角形的外心、垂心和重心都在同一直线上，而且外心和重心的距离是垂心和重心的距离之半”，这条直线被后人称之为三角形的欧拉线．若已知△ABC的顶点B（-1，0），C（0，2），且AB=AC，则△ABC的欧拉线方程为（　　）
A．2x-4y-3=0 B．2x+4y+3=0 C．4x-2y-3=0 D．2x+4y-3=0
组卷：71引用：5难度：0.7
解析
7．已知直线过点（1，2），且纵截距为横截距的两倍，则直线l的方程为（　　）
A．2x-y=0 B．2x+y-4=0
C．2x-y=0或x+2y-2=0 D．2x-y=0或2x+y-4=0
组卷：965引用：28难度：0.8
解析

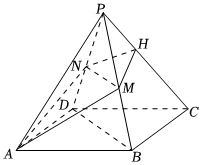21．已知四棱锥P-ABCD，底面ABCD为菱形，PD=PB，H为PC上的点，过AH的平面分别交PB，PD于点M，N，且BD∥平面AMHN．
（1）证明：MN⊥PC；
（2）当H为PC的中点，
PA
=
PC
=
3
AB
，PA与平面ABCD所成的角为60°，求平面PAM与平面AMN所成的锐二面角的余弦值．
组卷：208引用：12难度：0.6
解析
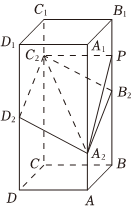22．如图，在正四棱柱ABCD-A₁B₁C₁D₁中，AB=2，AA₁=4．点A₂，B₂，C₂，D₂分别在棱AA₁，BB₁，CC₁，DD₁上，AA₂=1 BB₂=DD=2，CC₂=3．
（1）求多面体A₂B₂C₂D₂A₁的体积；
（2）当点P在棱BB₁上运动时（包括端点），求二面角P-A₂C₂-B₂的余弦值的绝对值的取值范围．
组卷：73引用：4难度：0.5
解析