2022-2023学年陕西省西安市雁塔二中七年级（下）第一次月考数学试卷

一、选择题（每小题3分，共30分）

• 1．计算（-3x³y）²正确的是（　　）

  A．6x6y2

  B．9x5y2

  C．9x6y2

  D．-3x3y2
  组卷：318引用：3难度：0.7

  解析

• 2．新型冠状病毒属于β属的新型冠状病毒，有包膜，颗粒呈圆形或者椭圆形，常为多形性，一个病毒的直径约为0.00000014m,用科学记数法可表示为（　　）

  A．0.14×10-6m

  B．1.4×10-6m

  C．1.4×10-7m

  D．1.4×10-8m
  组卷：212引用：6难度：0.8

  解析

• 3．已知α与β互为余角，若α=20°，则β的补角的大小为（　　）

  A．70°

  B．110°

  C．140°

  D．160°
  组卷：305引用：5难度：0.7

  解析

• 4．下列各式中，不能用平方差公式计算的是（　　）

  A．（-x-y）（x-y）	B．（-x+y）（-x-y）
  C．（x+y）（-x+y）	D．（x-y）（-x+y）
  组卷：2529引用：115难度：0.9

  解析

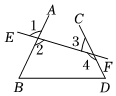• 5．如图，下列说法正确的是（　　）

  A．∠1和∠B是同位角	B．∠2和∠3是内错角
  C．∠3和∠4是对顶角	D．∠B和∠4是同旁内角
  组卷：3374引用：8难度：0.7

  解析

• 6．若a^m=2，aⁿ=5，则a^m+n等于（　　）

  A．7

  B．10

  C．25

  D．32
  组卷：1293引用：6难度：0.8

  解析

• 7．若二次三项式4x²+mxy+9y²是一个完全平方式，则m的可能值是（　　）

  A．±6

  B．12

  C．6

  D．±12
  组卷：1181引用：10难度：0.8

  解析

三、解答题（共7小题，共55分，解答应写出过程）

• 21．当我们利用两种不同的方法计算同一图形的面积时，可以得到一个等式，例如，由图1，可得等式：（a+2b）（a+b）=a²+3ab+2b²．
  
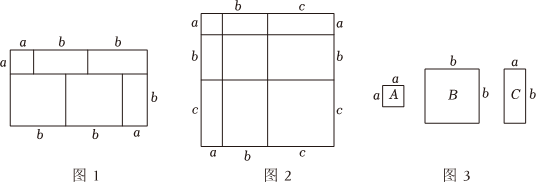
  （1）由图2，可得等式：

  ．
  （2）利用（1）中所得到的结论，解决下面的问题：已知a+b+c=12，ab+bc+ac=28，求a²+b²+c²的值．
  组卷：697引用：4难度：0.5

  解析

• 22．仔细阅读材料，再尝试解决问题：
  完全平方式x²±2xy+y²=（x±y）²以及（x±y）²的值为非负数的特点在数学学习中有广泛的应用，比如探求x²+6x+10的最大（小）值时，我们可以这样处理：
  例如：用配方法解题如下：x²+6x+10
  原式=x²+6x+9+1=（x+3）²+1
  因为无论x取什么数，都有（x+3）²的值为非负数，所以（x+3）²的最小值为0；此时x=-3时，进而（x+3）²+1的最小值是0+1=1；所以当x=-3时，原多项式的最小值是1．
  请根据上面的解题思路，探求：
  （1）若（x-5）²=0，则x=

  ．
  （2）已知x²+y²+2x-6y+10=0，求x+y的值．
  （3）已知多项式A为5x²+4y²+4xy-12x,问当x,y分别取何值时A有最小值？并求出A的最小值．
  组卷：610引用：4难度：0.6

  解析