2023-2024学年河南省信阳市八年级（上）期中数学试卷
发布：2024/10/2 8:0:1
一、选择题（每小题3分，共30分）下列各小题均有四个选项，其中只有一个是正确的.
-
1．以下四个标志，每个标志都有图案和文字说明，其中的图案是轴对称图形是（ ）
组卷：9引用：2难度：0.9 -
2．下列长度的各组线段首尾相接能构成三角形的是（ ）
组卷：235引用：7难度：0.9 -
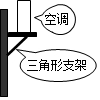3．如图，空调安装在墙上时，一般都会采用如图所示的方法固定，这种方法应用的几何原理是（ ）组卷：564引用：12难度：0.7 -
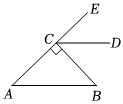4．如图，BC⊥AE，垂足为G，过C点作CD∥AB，若∠B=46°，则∠DCE的度数是（ ）组卷：186引用：3难度：0.5 -
5．已知点A的坐标为（3，-4），则点A关于y轴对称的点的坐标为（ ）
组卷：167引用：7难度：0.9 -
6．如图，小亮书上的三角形被墨迹污染了一部分，他根据所学全等三角形的知识很快就画了一个与书上完全一样的三角形，那么小亮画图的依据是（ ）组卷：121引用：5难度：0.6 -
7．已知一个多边形从一个顶点只可以引出四条对角线，那么它是（ ）
组卷：127引用：7难度：0.9
三、解答题（本大题共8个小题，共75分）
-
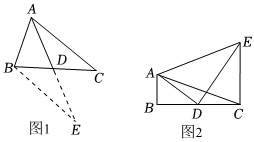22．数学兴趣小组在活动时，老师提出了这样一个问题：如图1，在△ABC中，AB=6，AC=8，D是BC的中点，求BC边上的中线AD的取值范围．小明在组内经过合作交流，得到了如下的解决方法：延长AD到点E，使DE=AD，请补充完整证明“△ADC≌△EDB”的推理过程．
（1）求证：△ADC≌△EDB．
证明：延长AD到点E，使DE=AD．
在△ADC和△EDB中，，AD=ED∠ADC=∠EDB（）CD=BD（中点定义）
∴△ADC≌△EDB（ ）．
（2）探究得出AD的取值范围是 ．
【感悟】解题时，条件中若出现“中点”“中线”等字样，可以考虑延长中线构造全等三角形，把分散的已知条件和所求证的结论集中到同一个三角形中．
【问题解决】
（3）如图2，在△ABC中，∠B=90°，AB=2，AD是△ABC的中线，CE⊥BC，CE=4，且∠ADE=90°，求AE的长．组卷：64引用：2难度：0.5 -
23．在等边△ABC中，点D为AC的中点，点F在BC延长线上，点E在射线AB上，∠EDF=120°．
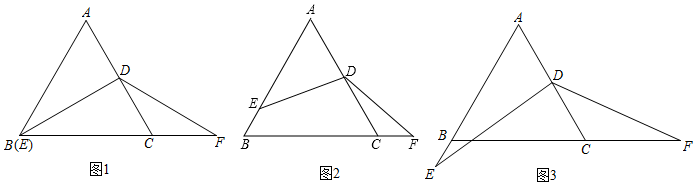
（1）如图1，当点E与点B重合时，则DE与DF的数量关系是 ；
（2）当点E在线段AB上时，（1）中的结论是否仍然成立？请结合图2说明理由；
（3）如图3，当点E在AB的延长线上时，BF=8，BE=2，请直接写出BC的长．组卷：241引用：5难度：0.2
