2021-2022学年贵州省铜仁五中八年级（下）期中数学试卷

一、选择题（每小题4分，共40分）

• 1．下列平面图形中，既是轴对称图形，又是中心对称图形的是（　　）

  A．

  B．

  C．

  D．
  组卷：212引用：24难度：0.9

  解析

• 2．四边形ABCD是平行四边形，若要它是正方形，则需要增加的条件是（　　）

  A．对角线相等	B．对角线垂直
  C．对角线垂直且相等	D．对角互补
  组卷：19引用：1难度：0.7

  解析

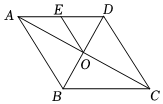• 3．菱形ABCD如图所示，对角线AC、BD相交于点O，若BD=6，菱形ABCD面积等于24，且点E为AD的中点，则线段OE的长为（　　）

  A．2

  B．2.5

  C．4

  D．5
  组卷：809引用：10难度：0.6

  解析

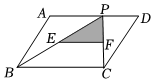• 4．如图，点P是平行四边形ABCD边AD上的一点，E，F分别是BP，CP的中点，已知平行四边形ABCD面积为24，那么△PEF的面积为（　　）

  A．12

  B．3

  C．6

  D．5
  组卷：13引用：1难度：0.6

  解析

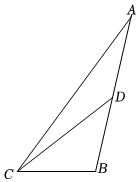• 5．如图，△ABC中，CD是AB边上的中线，AC=9cm,BC=3cm,那么△ACD和△BCD的周长的差是（　　）

  A．3cm

  B．6cm

  C．12cm

  D．无法确定
  组卷：1561引用：5难度：0.7

  解析

• 6．等腰三角形一边上的高等于这条边的一半，那么顶角是（　　）

  A．45°	B．30°或90°
  C．90°或150°	D．30°或90°或150°
  组卷：639引用：5难度：0.7

  解析

• 7．以不在同一直线上的三点为顶点作平行四边形，则第4个顶点的位置有（　　）

  A．1个

  B．2个

  C．.3个

  D．4个
  组卷：4引用：1难度：0.7

  解析

• 8．如图，将一副三角板在平行四边形ABCD中作如下摆放，设∠1=30°，那么∠2=（　　）

  A．55°

  B．65°

  C．75°

  D．85°
  组卷：2205引用：21难度：0.5

  解析

三、解答题（共86分）

• 23．取一张A4的纸按图操作：
  第一步：先把矩形ABCD对折，折痕为MN，如图（1）所示；
  第二步：再把B点叠在折痕线MN上，折痕为AE，点B在MN上的对应点为B'得Rt△AB'E，如图（2）所示；
  第三步：沿EB'线折叠得折痕EF，点A在直线EC上，如图（3）所示．
  利用展开图（4）探究：△AEF是什么三角形并证明你的结论．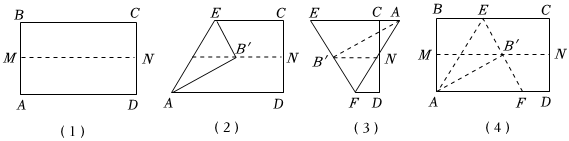
  
  组卷：23引用：1难度：0.6

  解析

• 24．已知△ABC是等腰直角三角形，∠ACB=90°，直线m是过点C的任一条直线，AE⊥m于点E，BD⊥m于点D；
  （1）如图（1），求证：AE=DE-BD；
  （2）当直线m绕点C旋转到如图（2）时，上述（1）中结论是否还成立？若不成立，请写出AE与DE和BD的正确数量关系，并加以证明．
  （3）当直线m绕点C旋转到如图（3）时，请直接写出AE与DE和BD的数量关系．
  
  组卷：7引用：1难度：0.4

  解析